Bài 36 trang 60 SGK Đại số 10 nâng cao

Vẽ đồ thị của mỗi hàm số sau:

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Vẽ đồ thị của mỗi hàm số sau:

LG a

\(y = \left\{ \matrix{
- x + 1\,\,\,\,\,\,\,\,;x \le - 1 \hfill \cr
- {x^2} + 3\,\,\,\,\,;x > - 1 \hfill \cr} \right.\)

Lời giải chi tiết:

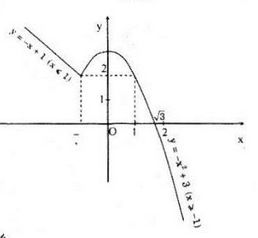
* Vẽ đường thẳng y = -x + 1 qua A(1, 0) và B(-1, 2)

* Vẽ parabol y = -x² + 3 có:

+ Đỉnh I(0, 3)

+ Trục đối xứng Oy

+ Đi qua điểm (1;2), cắt Oy tại (0;3)

Đồ thị cần vẽ gồm hai phần:

+ Phần đường thẳng ứng với \(x\le -1\), tức là để lại phần này và xóa phần đường thẳng ứng với x > -1 đi.

+ Phần parabol ứng với x > -1, tức là để lại phần này và xóa phần ứng với \(x\le -1\) đi.

Đồ thị:

LG b

\(y = \left\{ \matrix{
{1 \over 2}{(x + 3)^2}\,\,\,\,\,\,\,\,\,\,\,;x \le - 1 \hfill \cr
2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x > - 1 \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có:

\(y = \left\{ \begin{array}{l}
\frac{1}{2}{x^2} + 3x + \frac{9}{2}\,voi\,x \le - 1\\
2\,voi\,x > - 1
\end{array} \right.\)

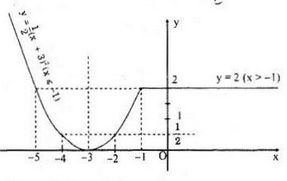
* Vẽ parabol \(y = \frac{1}{2}{x^2} + 3x + \frac{9}{2}\)

+ Đỉnh (-3;0)

+ Trục đối xứng x=-3.

+ Đi qua điểm (-1;2), (-5;2).

* Vẽ đường thẳng y=2 (song song với trục Ox và đi qua điểm (0;2)

Phần đồ thị cần tìm là hợp của hai phần sau:

+ parabol \(y = \frac{1}{2}{x^2} + 3x + \frac{9}{2}\) ứng với \(x\le -1\)

+ Nừa đường thẳng y=2 ứng với x > -1.

Đồ thị hàm số:

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Bài 37 trang 60 SGK Đại số 10 nâng cao
Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.
Bài 38 trang 61 SGK Đại số 10 nâng cao
Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).
Bài 35 trang 60 SGK Đại số 10 nâng cao
Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:
Bài 34 trang 60 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị hàm số tại y = ax2 + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:
Bài 33 trang 60 SGK Đại số 10 nâng cao
Lập bảng theo mẫu sau rồi điền vào ô trống các giá trị thích hợp (nếu có):
Bài 32 trang 59 SGK Đại số 10 nâng cao
Tìm tập hợp các giá trị x sao cho y > 0.
Bài 31 trang 59 SGK Đại số 10 nâng cao
Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0
Giải bài 30 trang 59 SGK Đại số 10 Nâng cao
Viết mỗi hàm số sau đây thành dạng y = a(x - p)2 + q
Bài 29 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = a(x - m)2. Tìm a và m trong mỗi trường hợp sau.
Bài 28 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = ax2 + c. Tìm a và c trong mỗi trường hợp sau:
Bài 27 trang 58 SGK Đại số 10 nâng cao
Không vẽ đồ thị, hãy mô tả đồ thị của mỗi hàm số trên bằng cách điền vào chỗ trống (...) theo mẫu: