Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

Bài 3: Hàm số bậc hai

Bài 35 trang 60 SGK Đại số 10 nâng cao

Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:

Lựa chọn câu để xem lời giải nhanh hơn

Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:

LG a

\(y = \,|{x^2} + \sqrt 2 x|\)

Phương pháp giải:

Đồ thị hàm số y=|f(x)| có được từ đồ thị hàm số y=f(x) như sau:

+) Giữ nguyên phần đồ thị phía trên trục Ox.

+) Lấy đối xứng phần dưới qua Ox và xóa phần dưới cũ đi.

Lời giải chi tiết:

Vẽ đồ thị hàm số \(y = \,{x^2} + \sqrt 2 x\) (P₁) rồi suy ra đồ thị hàm số: \(y = \,|{x^2} + \sqrt 2 x|\) (P)

Hoành độ của đỉnh: \({x_0} = - {b \over {2a}} = {{ - \sqrt 2 } \over 2}\)\( \Rightarrow {y_0} = {\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} + \sqrt 2 .\left( { - \frac{{\sqrt 2 }}{2}} \right)\)\(= {1 \over 2} - 1 = - {1 \over 2}\)

Đỉnh \(I( - {{\sqrt 2 } \over 2}; - {1 \over 2})\)

Bảng giá trị:

x	-1	\( - {{\sqrt 2 } \over 2}\)	0
y	\(1 - \sqrt 2 \)	\( - {1 \over 2}\)	0

Đồ thị hàm số:

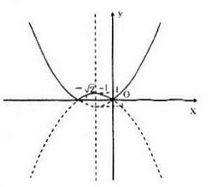
Ta giữ nguyên phần đồ thị trên trục hoành và lấy đối xứng phần đồ thị của hàm số \(y = \,{x^2} + \sqrt 2 x\) phía dưới trục hoành qua Ox ta được đồ thị của hàm \(y = \,|{x^2} + \sqrt 2 x|\) ( đồ thị là phần nét liền trên hình vẽ)

Bảng biến thiên:

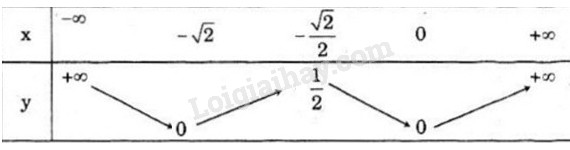
LG b

y = -x² + 2|x| + 3

Lời giải chi tiết:

Vẽ đồ thị hàm số y = -x² + 2x + 3 (P₁) rồi suy ra đồ thị hàm số: y = -x² + 2|x| + 3 (P)

Hoành độ đỉnh: \({x_0} = - {b \over {2a}} = {{ - 2} \over { - 2}} = 1 \Rightarrow {y_0} = 4\)

Đỉnh I (1, 4)

Bảng giá trị:

x	0	1	2
y	3	4	3

Đồ thị hàm số:

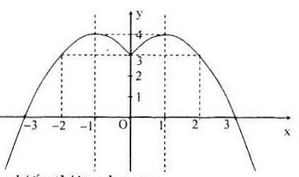
Bảng biến thiên

LG c

y = 0,5x² - |x – 1| + 1

Lời giải chi tiết:

y = 0,5x² - |x – 1| + 1

Ta có:

\(y = \left\{ \matrix{
0,5{x^2} - x + 2\,\,\,\,\,\,\,;x \ge 1 \hfill \cr
0,5{x^2} + x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x < 1 \hfill \cr} \right.\)

Đồ thị hàm số:

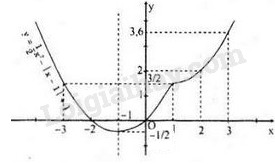
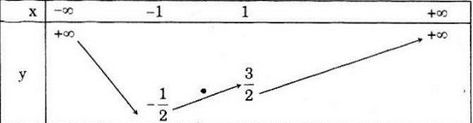
Bảng biến thiên:

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 16 phiếu

Bài tiếp theo

Bài 36 trang 60 SGK Đại số 10 nâng cao
Vẽ đồ thị của mỗi hàm số sau:
Bài 37 trang 60 SGK Đại số 10 nâng cao
Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.
Bài 38 trang 61 SGK Đại số 10 nâng cao
Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).
Bài 34 trang 60 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị hàm số tại y = ax2 + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:
Bài 33 trang 60 SGK Đại số 10 nâng cao
Lập bảng theo mẫu sau rồi điền vào ô trống các giá trị thích hợp (nếu có):
Bài 32 trang 59 SGK Đại số 10 nâng cao
Tìm tập hợp các giá trị x sao cho y > 0.
Bài 31 trang 59 SGK Đại số 10 nâng cao
Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0
Giải bài 30 trang 59 SGK Đại số 10 Nâng cao
Viết mỗi hàm số sau đây thành dạng y = a(x - p)2 + q
Bài 29 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = a(x - m)2. Tìm a và m trong mỗi trường hợp sau.
Bài 28 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = ax2 + c. Tìm a và c trong mỗi trường hợp sau:
Bài 27 trang 58 SGK Đại số 10 nâng cao
Không vẽ đồ thị, hãy mô tả đồ thị của mỗi hàm số trên bằng cách điền vào chỗ trống (...) theo mẫu: