Bài 34 trang 60 SGK Đại số 10 nâng cao

Gọi (P) là đồ thị hàm số tại y = ax2 + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:

Lựa chọn câu để xem lời giải nhanh hơn

Gọi (P) là đồ thị hàm số tại y = ax² + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:

LG a

(P) nằm hoàn toàn ở phía trên trục hoành

Phương pháp giải:

Nhận xét dựa vào bề lõm và đỉnh của parabol.

Lời giải chi tiết:

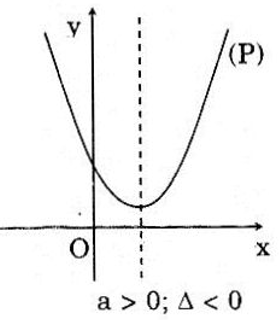
(P) nằm hoàn toàn phía trên trục hoành thì bề lõm hướng lên và đỉnh \(I( - {b \over {2a}};-{\Delta \over {4a}})\) nằm phía trên trục hoành nên

\(\left\{ \begin{array}{l}
a > 0\\
- \frac{\Delta }{{4a}} > 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a > 0\\
\Delta < 0
\end{array} \right.\)

Cách khác:

(P) nằm hoàn toàn phía trên trục hoành thì:

+) Bề lõm hướng lên nên \(a > 0\)

+) (P) nằm hoàn toàn phía trên trục hoành nghĩa là \(\left( P \right) \cap Ox = \emptyset \) hay phương trình \(a{x^2} + bx + c = 0\) vô nghiệm \( \Leftrightarrow \Delta < 0\)

Vậy \(a > 0,\Delta < 0\)

LG b

(P) nằm hoàn toàn ở phía dưới trục hoành

Lời giải chi tiết:

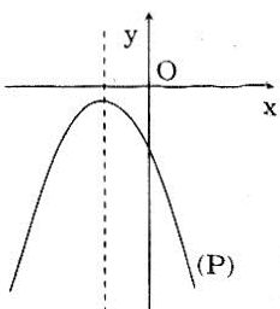
(P) nằm hoàn toàn phía dưới trục hoành thì:

+) bề lõm hướng xuống nên \(a < 0\).

+) đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) nằm phía dưới trục hoành nên \( - \frac{\Delta }{{4a}} < 0 \Leftrightarrow \frac{\Delta }{{4a}} > 0 \Leftrightarrow \Delta < 0\)

(vì \(a < 0\))

Vậy (P) nằm hoàn toàn phía dưới trục hoành thì a < 0 và Δ < 0.

LG c

(P) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành

Lời giải chi tiết:

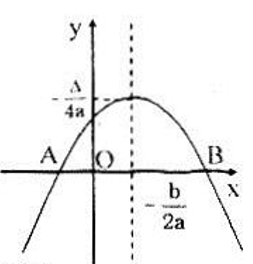
(P) phải có hình dạng ở hình vẽ trên, do đó phương trình ax² + bx + c = 0 có hai nghiệm phân biệt ⇔ Δ > 0

Đỉnh của (P) nằm phía trên trục hoành nên

\( - \frac{\Delta }{{4a}} > 0 \Leftrightarrow \frac{\Delta }{{4a}} < 0\)

Do đó \(\Delta\) và a trái dấu nên a < 0 (do Δ > 0)

Vậy (P) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành thì a < 0 và Δ > 0.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 20 phiếu

Bài tiếp theo

Bài 35 trang 60 SGK Đại số 10 nâng cao
Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:
Bài 36 trang 60 SGK Đại số 10 nâng cao
Vẽ đồ thị của mỗi hàm số sau:
Bài 37 trang 60 SGK Đại số 10 nâng cao
Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.
Bài 38 trang 61 SGK Đại số 10 nâng cao
Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).
Bài 33 trang 60 SGK Đại số 10 nâng cao
Lập bảng theo mẫu sau rồi điền vào ô trống các giá trị thích hợp (nếu có):
Bài 32 trang 59 SGK Đại số 10 nâng cao
Tìm tập hợp các giá trị x sao cho y > 0.
Bài 31 trang 59 SGK Đại số 10 nâng cao
Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0
Giải bài 30 trang 59 SGK Đại số 10 Nâng cao
Viết mỗi hàm số sau đây thành dạng y = a(x - p)2 + q
Bài 29 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = a(x - m)2. Tìm a và m trong mỗi trường hợp sau.
Bài 28 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = ax2 + c. Tìm a và c trong mỗi trường hợp sau:
Bài 27 trang 58 SGK Đại số 10 nâng cao
Không vẽ đồ thị, hãy mô tả đồ thị của mỗi hàm số trên bằng cách điền vào chỗ trống (...) theo mẫu: