Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

Bài 3: Hàm số bậc hai

Bài 32 trang 59 SGK Đại số 10 nâng cao

Tìm tập hợp các giá trị x sao cho y > 0.

Lựa chọn câu để xem lời giải nhanh hơn

Với mỗi hàm số y = -x² + 2x + 3 và \(y = {1 \over 2}{x^2} + x - 4\) , hãy:

LG a

Vẽ đồ thị của mỗi hàm số.

Lời giải chi tiết:

y = -x² + 2x + 3

\(a=-1, b=2, c=3\)

\(\begin{array}{l}
- \frac{b}{{2a}} = - \frac{2}{{2.\left( { - 1} \right)}} = 1\\
y\left( 1 \right) = - {1^2} + 2.1 + 3 = 4
\end{array}\)

Tọa độ đỉnh I(1, 4)

Trục đối xứng x=1

Bảng giá trị:

x	0	1	-1	3
y	3	4	0	0

Đồ thị:

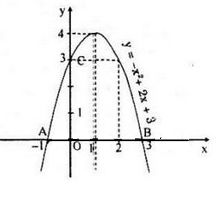
\(y = 0 ⇔ x = -1\) hoặc \(x = 3\)

+) Hàm số \(y = {1 \over 2}{x^2} + x - 4\)

\(a = \frac{1}{2},b = 1,c = - 4\)

\(\begin{array}{l}
- \frac{b}{{2a}} = - \frac{1}{{2.\frac{1}{2}}} = - 1\\
y\left( { - 1} \right) = - \frac{9}{4}
\end{array}\)

Tọa độ đỉnh \(I( - 1; - {9 \over 2})\)

Trục đối xứng: x=-1.

Bảng giá trị:

x	-1	0	2	-4
y	\( - {9 \over 2}\)	-4	0	0

Đồ thị hàm số:

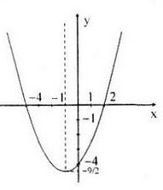
Đồ thị:

\(y = 0 \Leftrightarrow {1 \over 2}{x^2} + x - 4 = 0 \)

\(\Leftrightarrow \left[ \matrix{
x = 2 \hfill \cr
x = - 4 \hfill \cr} \right.\)

LG b

Tìm tập hợp các giá trị x sao cho y > 0.

Lời giải chi tiết:

Hàm số y = -x² + 2x + 3 có: \(y > 0 ⇔ -1 < x < 3\)

Hàm số \(y = {1 \over 2}{x^2} + x - 4\) có:

\(y > 0 ⇔ x < -4\) hoặc \(x > 2\)

LG c

Tìm tập hợp các giá trị x sao cho y < 0.

Lời giải chi tiết:

Hàm số y = -x² + 2x + 3 có: \(y < 0 ⇔ x < -1\) hoặc \(x > 3\)

Hàm số: \(y = {1 \over 2}{x^2} + x - 4\) có \(y < 0 ⇔ -4 < x < 2\)

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4 trên 7 phiếu

Bài tiếp theo

Bài 33 trang 60 SGK Đại số 10 nâng cao
Lập bảng theo mẫu sau rồi điền vào ô trống các giá trị thích hợp (nếu có):
Bài 34 trang 60 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị hàm số tại y = ax2 + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:
Bài 35 trang 60 SGK Đại số 10 nâng cao
Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:
Bài 36 trang 60 SGK Đại số 10 nâng cao
Vẽ đồ thị của mỗi hàm số sau:
Bài 37 trang 60 SGK Đại số 10 nâng cao
Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.
Bài 38 trang 61 SGK Đại số 10 nâng cao
Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).
Bài 31 trang 59 SGK Đại số 10 nâng cao
Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0
Giải bài 30 trang 59 SGK Đại số 10 Nâng cao
Viết mỗi hàm số sau đây thành dạng y = a(x - p)2 + q
Bài 29 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = a(x - m)2. Tìm a và m trong mỗi trường hợp sau.
Bài 28 trang 59 SGK Đại số 10 nâng cao
Gọi (P) là đồ thị của hàm số y = ax2 + c. Tìm a và c trong mỗi trường hợp sau:
Bài 27 trang 58 SGK Đại số 10 nâng cao
Không vẽ đồ thị, hãy mô tả đồ thị của mỗi hàm số trên bằng cách điền vào chỗ trống (...) theo mẫu: