Toán 10 Nâng cao

Bài 2: Hàm số bậc nhất

Bài 22 trang 53 SGK Đại số 10 nâng cao

Bình chọn:

3.8 trên 4 phiếu

Tìm bốn hàm số bậc nhất của đồ thị là bốn đường thẳng đôi một cắt nhau tại bốn đỉnh của một hình vuông nhận gốc O làm tâm đối xứng, biết rằng một đỉnh của hình vuông này là A (3 ; 0).

Xem thêm: Bài 2: Hàm số bậc nhất

Đề bài

Tìm bốn hàm số bậc nhất của đồ thị là bốn đường thẳng đôi một cắt nhau tại bốn đỉnh của một hình vuông nhận gốc O làm tâm đối xứng, biết rằng một đỉnh của hình vuông này là A (3 ; 0).

Lời giải chi tiết

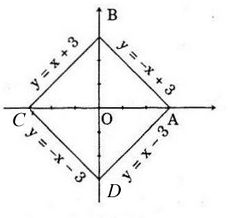
Vì O là tâm đối xứng của hình vuông và có đỉnh \(A(3; 0)\) nên các đỉnh còn lại của hình vuông là: \(B(0; 3); C(-3; 0); D(0; -3)\)

Đường thẳng đi qua hai điểm A, B có dạng \(y = ax + b\)

\(A(3; 0); B(0; 3)\) nằm trên đường thẳng nên:

\(\left\{ \matrix{
0 = 3a + b \hfill \cr
3 = b \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - 1 \hfill \cr
b = 3 \hfill \cr} \right.\)

Vậy AB: \(y= -x + 3\)

Tương tự:

BC: \(y = x + 3\)

CD: \(y = -x – 3\)

DA: \(y = x - 3\)

Loigiaihay.com

Bài tiếp theo

Báo lỗi - Góp ý

Các bài liên quan: - Bài 2: Hàm số bậc nhất

Bài 23 trang 53 SGK Đại số 10 nâng cao

Bài 23 trang 53 SGK Đại số 10 nâng cao

Khi tịnh tiến (G) sang phải 2 đơn vị, rồi xuống dưới 1 đơn vị, ta được đồ thị của hàm số nào?

Bài 24 trang 53 SGK Đại số 10 nâng cao

Bài 24 trang 53 SGK Đại số 10 nâng cao

Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng tọa độ và nêu nhận xét về quan hệ giữa chúng:

Bài 25 trang 54 SGK Đại số 10 nâng cao

Bài 25 trang 54 SGK Đại số 10 nâng cao

Hãy biểu diễn y như một hàm số bậc nhất trên từng khoảng ứng với đoạn [0 ; 10] và khoảng (10 ; +∞)

Bài 26 trang 54 SGK Đại số 10 nâng cao

Bài 26 trang 54 SGK Đại số 10 nâng cao

Bằng cácg bỏ dấu giá trị tuyệt đối, hãy viết hàm số đã cho dưới dạng hàm số bậc nhất trên từng khoảng.

Xem chi tiết

>>Học trực tuyến Lớp 10 trên Tuyensinh247.com, mọi lúc, mọi nơi tất cả các môn. Các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu

Các bài khác cùng chuyên mục

Tải app để xem offline!

Gửi văn hay nhận ngay phần thưởng

Các tác phẩm khác

Gửi bài tập - Có ngay lời giải