Bài 1 trang 45 SGK Hình học 12 Nâng cao

Trong không gian cho ba đoạn thẳng AB, BC, CD sao cho . Chứng minh rằng có mặt cầu đi qua bốn điểm A, B, C, D. Tính bán kính mặt cầu đó

Đề bài

Trong không gian cho ba đoạn thẳng \(AB, BC, CD\) sao cho \(AB \bot BC\,\,,\,\,BC \bot CD\,\,,\,\,CD \bot AB\) . Chứng minh rằng có mặt cầu đi qua bốn điểm \(A, B, C, D\). Tính bán kính mặt cầu đó nếu \(AB = a\,\,,\,\,BC = b\,\,,\,\,CD = c\) .

Quảng cáo

Lời giải chi tiết

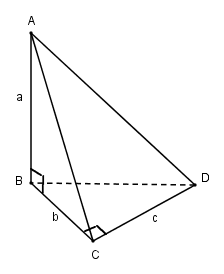
Vì \(AB \bot BC\) và \(AB \bot CD\) nên \(AB \bot \left( {BCD} \right)\). Suy ra \(AB \bot BD\)

Vì \(CD \bot BC\) và \(CD \bot AB\) nên \(CD \bot \left( {ABC} \right) \Rightarrow CD \bot AC\)

Gọi \(I\) là trung điểm \(AD\), ta có \(IB = IA = ID = IC\) nên các điểm \(A, B, C, D\) cùng nằm trên mặt cầu đường kính \(AD\).

Mặt khác ta có: \(A{D^2} = A{B^2} + B{D^2} \) \(= A{B^2} + B{C^2} + C{D^2}\) \( = {a^2} + {b^2} + {c^2}\)

\( \Rightarrow AD = \sqrt {{a^2} + {b^2} + {c^2}} \)

Do đó bán kính mặt cầu là \(R = {1 \over 2}AD = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.4 trên 5 phiếu

Bài tiếp theo

Bài 2 trang 45 SGK Hình học 12 Nâng cao
a) Tìm tập hợp tâm các mặt cầu đi qua hai điểm phân biệt A, B cho trước. b) Tìm tập hợp tâm các mặt cầu đi qua hai điểm phân biệt A, B, C cho trước. c) Tìm tập hợp tâm các mặt cầu đi qua một đường tròn cho trước. d) Có hay không một mặt cầu đi qua một đường tròn và một điểm nằm ngoài mặt phẳng chứa đường tròn.
Bài 3 trang 45 SGK Hình học 12 Nâng cao
Cho điểm M nằm trong mặt cầu (S). Trong các mệnh đề sau đây, mệnh đề nào đúng?
Bài 4 trang 45 SGK Hình học 12 Nâng cao
Cho đường thẳng d và điểm A không nằm trên d. Xét các mặt cầu đi qua A và có tâm nằm trên d. Chứng minh rằng các mặt cầu đó luôn đi qua một đường tròn cố định.
Bài 5 trang 45 SGK Hình học 12 Nâng cao
Trong các mệnh đề sau đây, mệnh đề nào đúng? a) Nếu hình đa diện nội tiếp mặt cầu thì mọi mặt của nó là đa giác nội tiếp đường tròn. b) Nếu tất cả các mặt của một hình đa diện nội tiếp đường tròn thì đa diện đó nội tiếp mặt cầu.
Bài 6 trang 45 SGK Hình học 12 Nâng cao
a) Tìm tập hợp các mặt cầu tiếp xúc với ba cạnh của một tam giác cho trước. b) Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện ABCD
Bài 7 trang 45 SGK Hình học 12 Nâng cao
a) Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng h. b) Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh cùng bằng a. Gọi A’, B’, C’, D’ lần lượt là trung điểm của SA, SB, SC, SD. Chứng minh rằng các điểm A, B, C, D, A’, B’, C’, D’ cùng thuộc một mặt cầu và tính thể tích khối cầu đó.
Bài 8 trang 45 SGK Hình học 12 Nâng cao
Cho tứ diện ABCD với AB = CD = c, AC = BD = b, AD = BC = a. a) Tính diện tích mặt cầu ngoại tiếp tứ diện. b) Chứng minh rằng có một mặt cầu tiếp xúc với bốn mặt của hình tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện)
Bài 9 trang 46 SGK Hình học 12 Nâng cao
Tìm diện tích mặt cầu ngoại tiếp hình chóp S.ABC biết rằng SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Chứng minh rằng các điểm S, trọng tâm tam giác ABC và tâm mặt cầu ngoại tiếp hình chóp S.ABC thẳng hàng.
Bài 10 trang 46 SGK Hình học 12 Nâng cao
a) Chứng minh rằng một hình trụ lăng trụ có mặt cầu cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng với đáy là đa giác nội tiếp đường tròn. b) Trong số các hình hộp nội tiếp mặt cầu cho trước, hình hộp nào có diện tích toàn phần lớn nhất?