Bài 4. Làm tròn và ước lượng trang 48 SGK Toán 7 cánh d..

Lý thuyết Làm tròn và ước lượng Toán 7 Cánh diều

I. Làm tròn số

I. Làm tròn số

1. Số làm tròn

Ở nhiều tình huống, ta cần tìm 1 số thực xấp xỉ với số thực đã cho để tiện ghi nhớ, đo đạc, tính toán. Số thực tìm được như thế gọi là số làm tròn.

2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước

Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.

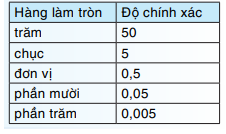
Khi làm tròn đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.

Ví dụ: Làm tròn số 2,13452….với độ chính xác 0,005, tức là làm tròn số 2,13452…. đến hàng phần trăm, ta được 2,13.

Chú ý: Trong đo đạc và tính toán, ta cố gắng làm tròn với độ chính xác càng nhỏ càng tốt.

II. Ước lượng

Đôi khi ta không quá quan tâm đến kết quả chính xác mà chỉ cần ước lượng kết quả, nghĩa là tìm một số gần sát với kết quả chính xác.

Ví dụ:

Ước lượng kết quả của phép tính: 49,87 . 1000,16

Ta ước lượng 49,87 . 1000,16 \( \approx \) 50 . 1000 = 50 000

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi khởi động trang 48 SGK Toán 7 tập 1 - Cánh diều
Một bồn hoa có dạng hình tròn với bán kính là 0,8 m. Hỏi diện tích của bồn hoa khoảng bao nhiêu mét vuông?
Giải mục I trang 48, 49 , 50 SGK Toán 7 tập 1 - Cánh diều
Hóa đơn tiền điện tháng 9/2020 của gia đình cô Hạnh là 574 880 đồng. Trong thực tế, cô Hạnh đã trả tiền mặt cho người thu tiền điện số tiền là 575 000 đồng. Tại sao cô Hạnh không thể trả cho người thu tiền điện số tiền chính xác là 574 880 đồng?
Giải mục II trang 50, 51 SGK Toán 7 tập 1 - Cánh diều
Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau: a) 18,25 + 11,98 b) 11,91 – 2,49 c) 30,09 . (-29,87)
Giải bài 1 trang 51 SGK Toán 7 tập 1 - Cánh diều
Làm tròn số 98 176 244 với độ chính xác 5 000.
Giải bài 2 trang 51 SGK Toán 7 tập 1 - Cánh diều
a) Làm tròn số 4,76908 với độ chính xác 0,5 b) Làm tròn số -4,76908 với độ chính xác 0,05.
Giải bài 3 trang 51 SGK Toán 7 tập 1 - Cánh diều
a) Sử dụng máy tính cầm tay để tính rồi viết mỗi số sau dưới dạng số thập phân vô hạn (tuần hoàn hoặc không tuần hoàn):
Giải bài 4 trang 51 SGK Toán 7 tập 1 - Cánh diều
Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau: a) (-28,29) + (- 11,91); b) 43,91 – 4,49; c) 60,49 . (-19,51).
Giải bài 5 trang 51 SGK Toán 7 tập 1 - Cánh diều
Các nhà khoa học tính được vận tốc ánh sáng bằng 299 792 458 m/s. Để dễ nhớ, người ta nói vận tốc ánh sáng là 300 000 000 m/s. Số liệu đó đã được làm tròn đến hàng nào?