 Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
 Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng t..
Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng t..
Giải mục 1 trang 80, 81 SGK Toán 7 tập 1 - Kết nối tri thức
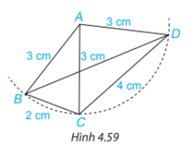
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
Câu hỏi
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
Phương pháp giải:
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau đó gọi là 2 cạnh bên, cạnh còn lại của tam giác gọi là cạnh đáy.
Lời giải chi tiết:
+) Tam giác ABD cân tại đỉnh A có:
AB, AD là 2 cạnh bên
BD là cạnh đáy
\(\widehat B,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ADC cân tại A có:
AC, AD là 2 cạnh bên
DC là cạnh đáy
\(\widehat C,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ABC cân tại A có:
AB, AC là 2 cạnh bên
BC là cạnh đáy
\(\widehat C,\widehat B\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
HĐ 1
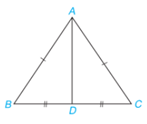
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
a) Chứng minh rằng \(\Delta \) ABD = \(\Delta \) ACD theo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Phương pháp giải:
a) Chứng minh ba cạnh của 2 tam giác trên bằng nhau
b) Từ câu a) suy ra 2 cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABD và ACD có:
AB = AC
AD chung
BD = DC
Do đó \(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\) (2 góc tương ứng)
HĐ 2
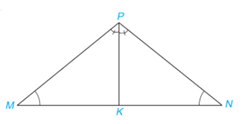
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
Phương pháp giải:
a) Sử dụng định lí: Tổng 3 góc trong một tam giác bằng 180 độ
b) Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh - góc
c) Sử dụng định nghĩa tam giác cân: Tam giác MNP cân là tam giác có 2 cạnh bằng nhau
Lời giải chi tiết:
a) Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^\circ}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^\circ}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b) Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
Suy ra \(\Delta MPK = \Delta NPK\) (g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
Do đó tam giác MNP cân tại P.
Luyện tập 1
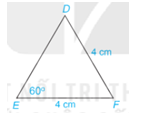
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
Phương pháp giải:
Chứng minh tam giác DEF cân tại F từ đó suy ra số đo các góc.
Lời giải chi tiết:
Cách 1: Vì tam giác DEF có DF = FE (= 4cm) nên tam giác DEF cân tại F.
Mà \(\widehat E=60^\circ\)
Do đó, \(\Delta DEF \) đều. (Tam giác cân có 1 góc bằng \(60^\circ\))
Suy ra \(\widehat D = \widehat F=\widehat E=60^\circ\).
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
Cách 2: Xét tam giác DEF có DF = FE (= 4cm) nên tam giác DEF cân tại F.
Suy ra \(\widehat E = \widehat D = {60^\circ}\) (tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^\circ}\\ {60^\circ} + {60^\circ} + \widehat F = {180^\circ}\\ \text{suy ra } \widehat F = {60^\circ}\end{array}\)
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
TTN
Một tam giác có gì đặc biệt nếu thoả mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau?
b) Tam giác cân có một góc bằng 60°?
Phương pháp giải:
Áp dụng: Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc ba góc bằng nhau.
Lời giải chi tiết:
a) Tam giác có ba góc bằng nhau là tam giác đều
b) Tam giác cân có 1 góc bằng 60 độ là tam giác đều.
- Giải mục 2 trang 81, 82, 83 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.23 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.24 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.25 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.26 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2












Danh sách bình luận