 Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
 Bài tập cuối chương IV trang 87 SGK Toán 7 kết nối tri ..
Bài tập cuối chương IV trang 87 SGK Toán 7 kết nối tri ..
Giải bài 4.38 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
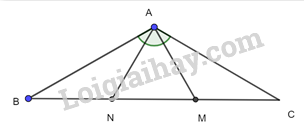
Cho tam giác ABC cân tại A có A= 120 . Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
Đề bài
Cho tam giác ABC cân tại A có \(\widehat {A} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Phương pháp giải - Xem chi tiết
a) Chứng minh 2 tam giác bằng nhau theo trường hợp g-c-g
b) Chứng minh tam giác có 2 cạnh bằng nhau hoặc 2 góc bằng nhau
Lời giải chi tiết
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^\circ)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
Do đó \(\Delta BAM = \Delta CAN\) (g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^\circ} - {{120}^\circ}}}{2} = {30^\circ}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^\circ}\\ {30^\circ} + {90^\circ} + \widehat {AMB} = {180^\circ}\\ \text{suy ra } \widehat {AMB} = {60^\circ}\\ \text{do đó } \widehat {AMC} = {180^\circ} - \widehat {AMB} = {180^\circ} - {60^\circ} = {120^\circ}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^\circ}\\ {120^\circ} + \widehat {MAC} + {30^\circ} = {180^\circ}\\ \text{suy ra } \widehat {MAC} = {30^\circ} = \widehat C\end{array}\)
Do đó tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\) nên BM=CN ( 2 cạnh tương ứng)
suy ra BM+MN=CN+NM
hay BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\) (do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
Suy ra \(\Delta ANB = \Delta AMC\) (c.c.c)
Mà tam giác AMC cân tại M nên tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^\circ} - {{120}^\circ}}}{2} = {30^\circ}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^\circ}\\ {30^\circ} + {90^\circ} + \widehat {AMB} = {180^\circ}\\ \text{suy ra } \widehat {AMB} = {60^\circ}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
Do đó \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
suy ra \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
\(\widehat{BAN} + 60^\circ=90^\circ\)
suy ra \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^\circ\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
\(\widehat{CAM} + 60^\circ=90^\circ\)
suy ra \(\widehat{CAM}=30^\circ\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^\circ\) nên \(\Delta ACM\) cân tại M.
- Giải bài 4.39 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.37 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.36 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.35 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
- Giải bài 4.34 trang 87 SGK Toán 7 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2












Danh sách bình luận