-
Chương 1: Số hữu tỉ - SBT KNTT
-
Chương 2: Số thực - SBT KNTT
-
Chương 3: Góc và đường thẳng song song - SBT KNTT
-
Chương 4: Tam giác bằng nhau - SBT KNTT
-
Chương 5: Thu thập và biểu diễn dữ liệu - SBT KNTT
-
Chương 6. Tỉ lệ thức và đại lượng tỉ lệ - SBT KNTT
-
Chương 7. Biểu thức đại số và đa thức một biến - SBT KNTT
-
Chương 8. Làm quen với biến cố và xác suất của biến cố
-
Chương 9. Quan hệ giữa các yếu tố trong một tam giác - SBT KNTT
-
Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam giác
-
Bài 32. Quan hệ giữa đường vuông góc và đường xiên
-
Bài 33. Quan hệ giữa ba cạnh của tam giác
-
Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
-
Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
-
Ôn tập chương 9
-
-
Chương 10. Một số hình khối trong thực tiễn - SBT KNTT
-
Bài tập cuối năm
Giải bài 4.27 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
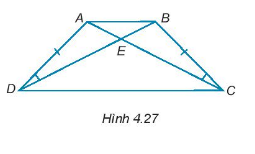
Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC
Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
Đề bài
Cho các điểm A, B, C, D, E như Hình 4.27, biết rằng AD = BC, \(\widehat {ADE} = \widehat {BCE}\). Chứng minh rằng:
a) \(\widehat {DAC} = \widehat {CBD}\)
b) \(\Delta AED = \Delta BEC.\)
c) \(AB//DC\)
Phương pháp giải - Xem chi tiết
a) Áp dụng định lí tổng 3 góc trong tam giác.
b) \(\Delta AED = \Delta BEC.\)(g – c – g)
c)
-Chứng minh \(\widehat {ABE} = \widehat {EAB}\)
-Chứng minh \(\widehat {ECD} = \widehat {EDC}\)
-Sử dụng định lí tổng 3 góc trong tam giác chứng minh 2 góc ở vị trí so le trong bằng nhau.
Lời giải chi tiết
a) Áp dụng định lí tổng 3 góc trong tam giác ADE, ta có:
Ta có: \(\widehat {DAE} + \widehat {ADE} + \widehat {AED}=180^0\)
\(\widehat {CBE} +\widehat {BCE} + \widehat {BEC}=180^0\)
Mà \(\widehat {AED} = \widehat {BEC}\) (2 góc đối đỉnh); \(\widehat {ADE}=\widehat {BCE}\)(gt)
\( \Rightarrow \widehat {DAC} = \widehat {DAE} = \widehat {CBE} = \widehat {CBD}\).
b)
Xét \(\Delta AED\)và \(\Delta BEC\) có:
AD = BC
\(\widehat {ADE} = \widehat {BCE}\)(gt)
\(\begin{array}{l}\widehat {DAE} = \widehat {CBE}\left( {cmt} \right)\\ \Rightarrow \Delta AED = \Delta BEC\left( {g - c - g} \right)\end{array}\)
c)
Ta có: \(\Delta AED = \Delta BEC\left( {cmt} \right) \Rightarrow EA = EB,ED = EC\)(2 cạnh tương ứng)
\( \Rightarrow AC = EA + EC = EB + ED = BD\)
Ta có: \(\Delta ADB = \Delta BCA\left( {c - g - c} \right)\left( {do\,AD = BC,\widehat {ADB} = \widehat {BCA},DB = CA} \right)\)
Nên \(\widehat {ABD} = \widehat {BAC}\) ( 2 góc tương ứng)
Mặt khác: \(\Delta ADC = \Delta BCD\left( {c - c - c} \right)\left( {do\,AD = BC;AC = BD,DC:chung} \right)\)
Nên \(\widehat {ACD} = \widehat {BDC}\) ( 2 góc tương ứng)
Như vậy:
\(2\widehat {ABD} = \widehat {ABE} + \widehat {BAE} = {180^0} - \widehat {AEB} = {180^0} - \widehat {DEC} = \widehat {ECD} + \widehat {EDC} = 2\widehat {BDC}\)\(\)
Do đó:
\(\widehat {ABD} = \widehat {BDC}\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB// CD\) (Dấu hiệu nhận biết hai đường thẳng song song)
Bình luận
Chia sẻ
- Giải bài 4.28 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.29 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.26 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.25 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.24 trang 61 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải Bài 18 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 17 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 16 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 15 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 14 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 18 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 17 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 16 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 15 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 14 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
