 Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
 Ôn tập chương I
Ôn tập chương I
Câu 7 trang 34 SGK Hình học 11 Nâng cao
a. Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A
LG a
Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A tỉ số \(k = {{AB} \over {AM}}\) . Hãy dựng ảnh của hình vuông MNPQ qua phép vị tự V.
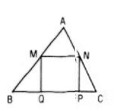
Lời giải chi tiết:
Ta có \(\overrightarrow {AB} = k\overrightarrow {AM} \) và \(\overrightarrow {AC} = k\overrightarrow {AN} \) nên phép vị tự V biến điểm M thành điểm B, biến điểm N thành điểm C.
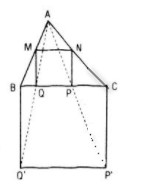
Vậy V biến hình vuông MNPQ thành hình vuông BCP’Q’ như trên hình dưới:
LG b
Từ bài toán ở câu a) hãy suy ra cách giải bài toán sau: Cho tamn giác nhọn ABC, hãy dựng hình vuông MNPQ sao cho hai đỉnh P, Q nằm trên cạnh BC và hai đỉnh M, N lần lượt nằm trên hai cạnh AB và AC
Lời giải chi tiết:
Dựng hình vuông BCP’Q’ nằm ngoài tam giác ABC như hình

Lấy giao điểm P, Q của BC với các đoạn thẳng tương ứng AP’ và AQ’
Từ P và Q, kẻ các đường thẳng vuông góc với BC, lần lượt cắt AC và AB tại N và M
Khi đó MNPQ chính là hình vuông cần dựng
Loigiaihay.com












Danh sách bình luận