-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Ôn tập chương I
Câu 5 trang 34 SGK Hình học 11 Nâng cao
Cho tam giác ABC nội tiếp trong đường tròn (O)
Đề bài
Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M1 là điểm đối xứng với M qua A, M2 là điểm đối xứng với M1 qua B, M3 là điểm đối xứng với M2 qua C
a. Chứng tỏ rằng phép biến hình F biến điểm M thành M3 là một phép đối xứng tâm
b. Tìm quỹ tích điểm M3
Lời giải chi tiết
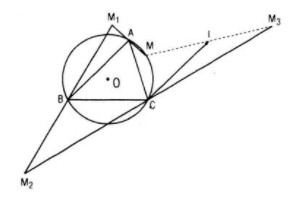
a. Gọi I là trung điểm của MM3, ta chứng minh I là điểm cố định
Thật vậy, ta có:
\(\eqalign{
& \overrightarrow {CI} = {1 \over 2}\left( {\overrightarrow {CM} + \overrightarrow {C{M_3}} } \right) \cr
& \,\,\,\,\,\,\, = {1 \over 2}\left( {\overrightarrow {CM} + \overrightarrow {{M_2}C} } \right) \cr
& \,\,\,\,\,\,\, = {1 \over 2}\overrightarrow {{M_2}M} = \overrightarrow {BA} \cr} \)
Như vậy điểm I cố định, do đó phép biến hình F biến M thành M3 là phép đối xứng qua điểm I
b. Quỹ tích điểm M3 là đường tròn (O’), ảnh của đường tròn (O) qua phép đối xứng tâm với tâm I
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 6 trang 34 SGK Hình học 11 Nâng cao
- Câu 7 trang 34 SGK Hình học 11 Nâng cao
- Câu 8 trang 35 SGK Hình học 11 Nâng cao
- Câu 9 trang 35 SGK Hình học 11 Nâng cao
- Câu 4 trang 34 SGK Hình học 11 Nâng cao .
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
