-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 2. Hoán vị, chỉnh hợp và tổ hợp
Câu 11 trang 63 SGK Đại số và Giải tích 11 Nâng cao
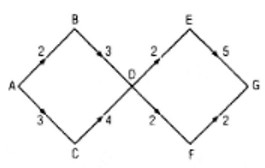
Xét mạng đường nối các tỉnh A, B, C, D, E, F, G, trong đó số viết trên một cạch cho biết số con đường nối hai tỉnh nằm ở hai
Đề bài
Xét mạng đường nối các tỉnh A, B, C, D, E, F, G, trong đó số viết trên một cạch cho biết số con đường nối hai tỉnh nằm ở haiđầu mút của cạnh (h. 2.2). Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh G ?
Phương pháp giải - Xem chi tiết
Liệt kê các trường hợp có thể đi từ A đến G.
Dùng quy tắc nhân đếm số cách đi trong từng TH.
Dùng quy tắc cộng suy ra số cách đi cần tìm.
Lời giải chi tiết
Có 4 phương án đi qua các tỉnh A đến G là :
a. A → B → D → E → G
b. A → B → D → F → G
c. A → C → D → E → G
d. A → C → D → F → G
Theo quy tắc nhân, ta có :
Phương án a: A → B → D → E → G
Có \(2.3.2.5 = 60\) cách đi;
Phương án b: A → B → D → F → G
Có \(2.3.2.2 = 24\) cách đi;
Phương án c: A → C → D → E → G
Có \(3.4.2.5 = 120\) cách đi;
Phương án d: A → C → D → F → G
Có \(3.4.2.2 = 48\) cách đi.
Theo quy tắc cộng, ta có : \(60 + 24 + 120 + 48 = 252\) cách đi từ A đến G.
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 12 trang 63 SGK Đại số và Giải tích 11 Nâng cao
- Câu 13 trang 63 SGK Đại số và Giải tích 11 Nâng cao
- Câu 14 trang 63 SGK Đại số và Giải tích 11 Nâng cao
- Câu 15 trang 64 SGK Đại số và Giải tích 11 Nâng cao
- Câu 16 trang 64 SGK Đại số và Giải tích 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
