Bài 9 trang 15 SGK Hình học 12 Nâng cao

Đề bài

Chứng minh rằng các phép tịnh tiến, đối xứng trục, đối xứng tâm là những phép dời hình.

Quảng cáo

Lời giải chi tiết

* Phép tịnh tiến

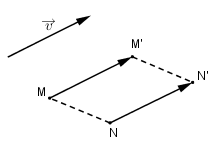
Giả sử \({T_{\overrightarrow v }}\) là phép tịnh tiến theo vectơ \(\overrightarrow v \)

\(\eqalign{
& {T_{\overrightarrow v }}:\,M \to M' \cr 
& \,\,\,\,\,\,\,\,N \to N' \cr} \)

Ta có \(\overrightarrow {MM'}  = \overrightarrow {NN'}  = \overrightarrow v\) nên MM'N'N là hình bình hành

\(  \Rightarrow \overrightarrow {MN}  = \overrightarrow {M'N'}  \Rightarrow MN = M'N'\)
Vậy phép tịnh tiến là một phép dời hình.
* Phép đối xứng trục

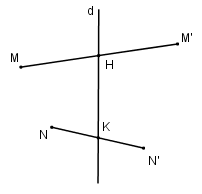
Giả sử \({\tilde N_d}\) là phép đối xứng qua đường thẳng \(d\)
Giả sử

\({{\tilde N}_d}:M \to M'\)

\(N \to N'\)

Gọi \(H\) và \(K\) lần lượt là trung điểm của \(MM’\) và \(NN’\).
Ta có:

\(\eqalign{
& \overrightarrow {MN} + \overrightarrow {M'N'}\cr & = \left( {\overrightarrow {MH} + \overrightarrow {HK} + \overrightarrow {KN} } \right) \cr & + \left( {\overrightarrow {M'H} + \overrightarrow {HK} + \overrightarrow {KN'} } \right) \cr & = \left( {\overrightarrow {MH}  + \overrightarrow {M'H} } \right) + \left( {\overrightarrow {KN}  + \overrightarrow {KN'} } \right) \cr & + \left( {\overrightarrow {HK}  + \overrightarrow {HK} } \right) \cr &  = \overrightarrow 0  + \overrightarrow 0  + 2\overrightarrow {HK} \cr &= 2\overrightarrow {HK} \cr 
& \overrightarrow {MN} - \overrightarrow {M'N'}\cr & = (\overrightarrow {HN} - \overrightarrow {HM} )- ( \overrightarrow {HN'} - \overrightarrow {HM'} )\cr & = \left( {\overrightarrow {HN}  - \overrightarrow {HN'} } \right) + \left( {\overrightarrow {HM'}  - \overrightarrow {HM} } \right)\cr &= \overrightarrow {N'N} + \overrightarrow {MM'} \cr} \)

Vì \(\overrightarrow {MM'}  \bot \overrightarrow {HK} \) và \(\overrightarrow {N'N}  \bot  \overrightarrow {HK} \) nên

\(\eqalign{
& {\overrightarrow {MN} ^2} - {\overrightarrow {M'N'} ^2} \cr &= \left( {\overrightarrow {MN} + \overrightarrow {M'N'} } \right)\left( {\overrightarrow {MN} - \overrightarrow {M'N'} } \right) \cr &= 2\overrightarrow {HK} \left( {\overrightarrow {N'N} + \overrightarrow {MM'} } \right) \cr &= 2\overrightarrow {HK} .\overrightarrow {N'N}  + 2\overrightarrow {HK} .\overrightarrow {MM'}  \cr &= 2.0 + 2.0 = 0 \cr 
& \Rightarrow M{N^2} = M'N{'^2} \Rightarrow MN = M'N' \cr} \)

Vậy phép đối xứng qua \(d\) là phép dời hình.

Cách khác:

Giả sử phép đối xứng qua đường thẳng d biến M thành M’, N thành N’

Gọi (P) là mặt phẳng chứa NM’ và (P) // MM’

\({M_1},{M_1}'\) lần lượt là hình chiếu của M, M’ trên (P); O = ∩(P).

Ta có d ⊥ (P) nên O đồng thời là trung điểm của \({M_1}{M_1}'\) và NN'.

Vậy phép đối xứng tâm O biến \(M_1\) thành \(M_1'\), N thành N’ nên \({M_1},{M_1}'\) nên \(M_1 N=M_1'N'\).

Mặt khác \(M_1 N,M_1'N'\) lần lượt là hình chiếu của MN, M’N’ trên (P), MM’ // (P) nên MN = M’N’.

Vậy phép đối xứng qua đường thẳng là phép dời hình.

* Phép đối xứng tâm
Nếu phép đối xứng qua tâm \(O\) biến hai điểm \(M, N\) lần lượt thành hai điểm \(M’, N’\) thì \(\overrightarrow {OM'}  =  - \overrightarrow {OM} ;\overrightarrow {ON'}  =  - \overrightarrow {ON} \)
suy ra \(\overrightarrow {M'N'}  = \overrightarrow {ON'}  - \overrightarrow {OM'}  \) \(  =  - \overrightarrow {ON}  + \overrightarrow {OM} = \overrightarrow {NM}  \) \(\Rightarrow M'N' = MN\)
Vậy phép đối xứng tâm \(O\) là một phép dời hình.

Loigiaihay.com