Bài 6 trang 15 SGK Hình học 12 Nâng cao

Gọi Đ là phép đối xứng qua mặt phẳng (P) và a là một đường thắng nào đó. Giả sử Đ biến đường thẳng a thành đường thẳng a’. Trong trường hợp nào thì : a) a trùng với a’ ; b) a song song với a’; c) a cắt a'; d) a và a' chéo nhau ?

Bài 6. Gọi \(Đ\) là phép đối xứng qua mặt phẳng \((P)\) và \(a\) là một đường thắng nào đó. Giả sử \(Đ\) biến đường thẳng \(a\) thành đường thẳng \(a’\). Trong trường hợp nào thì :

a) \(a\) trùng với \(a'\) ;

b) \(a\) song song với \(a'\);

c) \(a\) cắt \(a'\);

d) \(a\) và \(a'\) chéo nhau ?

Giải

a) \(a\) trùng với \(a’\) khi \(a\) nằm trên mp\((P)\) hoặc \(a\) vuông góc với mp\((P)\)

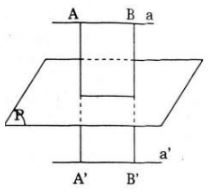
b) \(a\) song song với \(a’\) khi \(a\) song song với mp\((P)\).

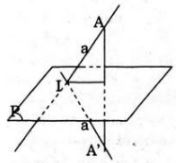
c) \(a\) cắt \(a’\) khi \(a\) cắt \(mp(P)\) nhưng không vuông góc với \(mp(P)\).

d) \(a\) và \(a’\) không bao giờ chéo nhau.

loigiaihay.com