Bài 38 trang 109 SGK Hình học 10 Nâng cao

Chứng minh rằng:

Đề bài

Cho đường tròn (C) tâm \({F_1}\) , bán kính R và một điểm \({F_2}\) ở ngoài (C). Chứng minh rằng tập hợp tâm các đường tròn đi qua \({F_2}\) , tiếp xúc với (C) là một đường hypebol. Viết phương trình chính tắc của hypebol đó.

Lời giải chi tiết

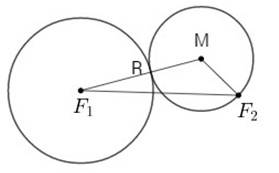
Gọi M là tâm đường tròn (C') đi qua \({F_2}\) và tiếp xúc với (C)

+) Nếu (C') tiếp xúc ngoài với (C) thì \(MF_1 - MF_2 = R\)

+) Nếu (C') tiếp xúc trong với (C) thì \(MF_2 - MF_1 = R\)

Do đó \(|M{F_1} - M{F_2}| = R = 2a\)

Vậy tập hợp các điểm M là đường hypebol (H) có \(a = {R \over 2},c = {{{F_1}{F_2}} \over 2}\)

\( \Rightarrow {b^2} = {c^2} - {a^2} = {{{F_1}{F_2}^2 - {R^2}} \over 4}\)

Phương trình chính tắc của (H) là:

\({{{x^2}} \over {{{\left( {{R \over 2}} \right)}^2}}} - {{{y^2}} \over {{{\left( {{{\sqrt {{F_1}{F_2}^2 - {R^2}} } \over 2}} \right)}^2}}} = 1.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Bài 39 trang 109 SGK Hình học 10 Nâng cao
Viết phương trình chính tắc của hypebol (H) trong mỗi trường hợp sau
Bài 40 trang 109 SGK Hình học 10 Nâng cao
Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.
Bài 41 trang 109 SGK Hình học 10 Nâng cao
Chứng minh rằng:
Bài 37 trang 109 SGK Hình học 10 Nâng cao
Tìm tọa độ các tiêu điểm, các đỉnh; độ dài trục thực, trục ảo và phương trình các đường tiệm cận của mỗi hypebol có phương trình sau
Bài 36 trang 108 SGK Hình học 10 Nâng cao
Hỏi trong các mệnh đề sau, mệnh đề nào đúng?