 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 3. Khoảng cách và góc
Bài 3. Khoảng cách và góc
Bài 20 trang 90 SGK Hình học 10 Nâng cao
Cho hai đường thẳng sau:
Đề bài
Cho hai đường thẳng
\(\eqalign{
& {\Delta _1}:x + 2y - 3 = 0 \cr
& {\Delta _2}:3x - y + 2 = 0 \cr} \)
Viết phương trình đường thẳng \(\Delta \) đi qua điểm P(3, 1) và cắt \({\Delta _1},{\Delta _2}\) lần lượt ở A,B sao cho \({\Delta}\) tạo với \({\Delta _1}\) và \({\Delta _2}\) một tam giác cân có cạnh đáy là AB.
Phương pháp giải - Xem chi tiết
\(\Delta \) cắt \({\Delta _1},{\Delta _2}\) ở A và B sao cho \({\Delta}\) tạo với \({\Delta _1}\) và \({\Delta _2}\) một tam giác cân có đáy AB thì góc hợp bởi \(\Delta \) với \({\Delta _1}\) và góc hợp bởi \(\Delta \) với \({\Delta _2}\) bằng nhau.
Do đó, cách làm như sau:
+) Giả sử \(\Delta \) qua P có vectơ pháp tuyến \(\overrightarrow n \left( {a;b} \right)\).
+) Tính \(\cos \left( {\Delta ,{\Delta _1}} \right) \) và \(\cos \left( {\Delta ,{\Delta _2}} \right)\)
+) Tìm mối quan hệ của a, b từ phương trình \(\cos \left( {\Delta ,{\Delta _1}} \right) = \cos \left( {\Delta ,{\Delta _2}} \right)\).
+) Chọn b=1, tìm a và suy ra phương trình đường thẳng.
Lời giải chi tiết
\({\Delta _1}\) có vectơ pháp tuyến là: \(\overrightarrow {{n_1}} \left( {1;2} \right).\)
\({\Delta _2}\) có vectơ pháp tuyến là: \(\overrightarrow {{n_2}} \left( {3; - 1} \right).\)
Giả sử \(\Delta \) qua P có vectơ pháp tuyến \(\overrightarrow n \left( {a;b} \right)\).
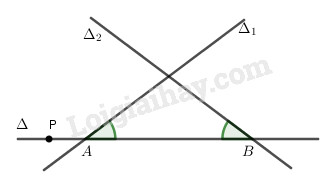
Từ hình vẽ ta thấy:
\(\Delta \) cắt \({\Delta _1},{\Delta _2}\) ở A và B sao cho \({\Delta}\) tạo với \({\Delta _1}\) và \({\Delta _2}\) một tam giác cân có đáy AB thì góc hợp bởi \(\Delta \) với \({\Delta _1}\) và góc hợp bởi \(\Delta \) với \({\Delta _2}\) bằng nhau.
Do đó,
\(\cos \left( {\Delta ,{\Delta _1}} \right) = \cos \left( {\Delta ,{\Delta _2}} \right)\)
\(\eqalign{
&\Leftrightarrow {{\left| {\overrightarrow {{n_1}} .\overrightarrow n } \right|} \over {\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow n } \right|}} = {{\left| {\overrightarrow {{n_2}} .\overrightarrow n } \right|} \over {\left| {\overrightarrow {{n_2}} } \right|.\left| {\overrightarrow n } \right|}} \cr
& \Leftrightarrow {{|a + 2b|} \over {\sqrt {{1^2} + {2^2}} }} = {{|3a - b|} \over {\sqrt {{3^2} + {1^2}} }} \cr
& \Leftrightarrow \frac{{\left| {a + 2b} \right|}}{{\sqrt 5 }} = \frac{{\left| {3a - b} \right|}}{{\sqrt {10} }}\cr &\Leftrightarrow \sqrt 2 |a + 2b| = |3a - b| \cr
& \Leftrightarrow 2{\left( {a + 2b} \right)^2} = {\left( {3a - b} \right)^2} \cr
& \Leftrightarrow 2\left( {{a^2} + 4ab + 4{b^2}} \right) = 9{a^2} - 6ab + {b^2}\cr & \Leftrightarrow 7{a^2} - 14ab - 7{b^2} = 0\cr &\Leftrightarrow {a^2} - 2ab - {b^2} = 0 \cr} \)
Chọn \(b = 1\) ta có: \({a^2} - 2a - 1 = 0 \Leftrightarrow a = 1 \pm \sqrt 2 \)
Loigiaihay.com













Danh sách bình luận