 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 3. Phép vị tự và sự đồng dạng của các khối đa diện...
Bài 3. Phép vị tự và sự đồng dạng của các khối đa diện...
Bài 12 trang 20 SGK Hình học 12 Nâng cao
Cho một khối tứ diện đều. Hãy chứng minh rằng: a) Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều. b) Các trung điểm của các cạnh của nó là các đỉnh của một khối tám mặt đều.
Cho một khối tứ diện đều. Hãy chứng minh rằng:
LG a
Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.
Lời giải chi tiết:
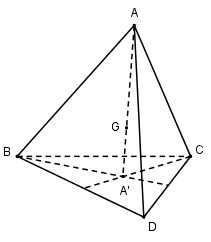
Gọi \(A’, B’, C’, D’\) lần lượt là trọng tâm của tam giác \(BCD, CDA, BDA, ABC\) của tứ diện đều \(ABCD\) có trọng tâm \(G\).
Ta có \(\overrightarrow {GA'} = - {1 \over 3}\overrightarrow {GA} \)
\(\overrightarrow {GB'} = - {1 \over 3}\overrightarrow {GB} \)
\(\overrightarrow {GC'} = - {1 \over 3}\overrightarrow {GC} \)
\(\overrightarrow {GD'} = - {1 \over 3}\overrightarrow {GD} \)
Gọi \({V_{\left( {G;{{ - 1} \over 3}} \right)}}\) là phép vị tự tâm \(G\) tỉ số \( - {1 \over 3}\) ta có \(A’, B’, C’, D’\) lần lượt là ảnh của \(A, B, C, D\) qua phép vị tự \(V\).
Từ đó suy ra phép vị tự tâm G tỉ số \(- {1 \over 3}\) biến tứ diện ABCD thành tứ diện A'B'C'D'.
Do đó nếu \(ABCD\) là tứ diện đều thì \(A’B’C’D’\) cũng là tứ diện đều.
LG b
Các trung điểm của các cạnh của nó là các đỉnh của một khối tám mặt đều.
Lời giải chi tiết:
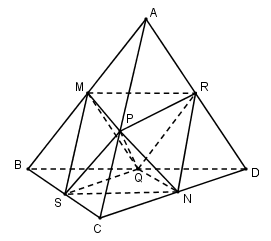
Gọi \(M, N, P, Q, R, S\) lần lượt là trung điểm của các cạnh \(AB, CD, AC, BD, AD, BC\) của khối tứ diện đều \(ABCD\).
Xét tam giác ABC có M, P, S lần lượt là trung điểm AB, AC, BC nên MP, PS, SM là đường trung bình của tam giác
Suy ra \(MP = \frac{1}{2}BC\), \(PS = \frac{1}{2}AB,SM = \frac{1}{2}AC\).
Mà tứ diện ABCD đều nên AB=BC=CA nên MP=PS=SM hay tma giác MPS đều.
Tương tự ta có các tam giác SPN, SQN, SQM, RPN, RNQ, RQM, RPM đều.
Khi đó, tám tam giác đều đó làm thành khối đa diện với các đỉnh là \(M, N, P, Q, R, S\) mà mỗi đỉnh là đỉnh chung của bốn cạnh.
Vậy đó là khối tám mặt đều.
Loigiaihay.com












Danh sách bình luận