Copyright © 2021 loigiaihay.com
CHƯƠNG 1. ĐA THỨC NHIỀU BIẾN
Bài 1. Đơn thức nhiều biến. Đa thức nhiều biến
Bài 2. Các phép tính với đa thức nhiều biến
Bài 3. Hằng đẳng thức đáng nhớ
Bài 4. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử
Bài tập cuối chương 1
CHƯƠNG 2. PHÂN THỨC ĐẠI SỐ
Bài 1. Phân thức đại số
Bài 2. Phép cộng, phép trừ phân thức đại số
Bài 3. Phép nhân, phép chia phân thức đại số
Bài tập cuối chương 2
Hoạt động thực hành và trải nghiệm Chủ đề 1. Quản lí tài chính cá nhân
CHƯƠNG 3. HÀM SỐ VÀ ĐỒ THỊ
Bài 1. Hàm số
Bài 2. Mặt phẳng tọa độ. Đồ thị của hàm số
Bài 3. Hàm số bậc nhất y=ax+b (a khác 0)
Bài 4. Đồ thị của hàm số bậc nhất y=ax+b(a khác 0)
Bài tập cuối chương 3
CHƯƠNG 4. HÌNH HỌC TRỰC QUAN
Bài 1. Hình chóp tam giác đều
Bài 2. Hình chóp tứ giác đều
Bài tập cuối chương 4
CHƯƠNG 5. TAM GIÁC. TỨ GIÁC
Bài 1. Định lí Pythagore
Bài 2. Tứ giác
Bài 3. Hình thang cân
Bài 4. Hình bình hành
Bài 5. Hình chữ nhật
Bài 6. Hình thoi
Bài 7. Hình vuông
Bài tập cuối chương 5
CHƯƠNG 6. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
Bài 1. Thu thập và phân loại dữ liệu
Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
Bài tập cuối chương 6
CHƯƠNG 7. PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1. Phương trình bậc nhất một ẩn
Bài 2. Ứng dụng của phương trình bậc nhất một ẩn
Bài tập cuối chương 7
CHƯƠNG 8. TAM GIÁC ĐỒNG DẠNG. HÌNH ĐỒNG DẠNG
Bài 1. Định lí Thalès trong tam giác
Bài 2. Ứng dụng của định lí Thalès trong tam giác
Bài 3. Đường trung bình của tam giác
Bài 4. Tính chất đường phân giác của tam giác
Bài 5. Tam giác đồng dạng
Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
Bài 7. Trường hợp đồng dạng thứ hai của tam giác
Bài 8. Trường hợp đồng dạng thứ ba của tam giác
Bài 9. Hình đồng dạng
Bài 10. Hình đồng dạng trong thực tiễn
Bài tập cuối chương 8
Trắc nghiệm Trường hợp cạnh - góc - cạnh Toán 8 có đáp án
Trắc nghiệm Trường hợp cạnh - góc - cạnh
14 câu hỏi
Trắc nghiệm
Câu 1 :
Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
-
A.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
một cạnh của tam giác này bằng một cạnh của tam giác kia và một cặp góc bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Câu 2 :
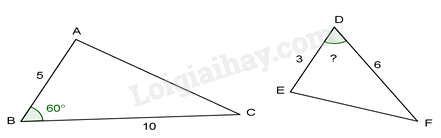
Cho \(\Delta D{\rm{EF}}\) và \(\Delta ILK\) , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)?}}\)
-
A.
\(\hat E = \hat I.\)
-
B.
\(\hat E = \hat L\)
-
C.
\(\hat P = \hat I.\)
-
D.
\(\hat F = \hat K\)
-
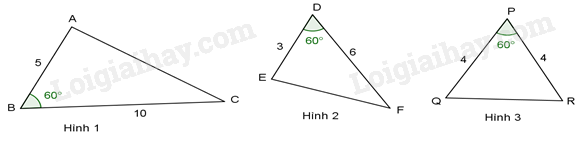
A.
Hình 1 và hình 2.
-
B.
Hình 2 và hình 3.
-
C.
Hình 1 và hình 3.
-
D.
Hình 1, hình 2 và hình 3.
-
A.
\({50^0}\)
-
B.
\({60^0}\)
-
C.
\({30^0}\)
-
D.
\({70^0}\)
Câu 5 :
Cho \(\Delta {A'}{B'}{C'}\) và \(\Delta ABC\) có \(\hat A = {\hat A'}\) . Để \(\Delta {A'}{B}{C'} \backsim \Delta ABC\) cần thêm điều kiện là:
-
A.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}.\)
-
B.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{B'}{C'}}}{{BC}}.\)
-
C.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{BC}}{{{B'}{C'}}}.\)
-
D.
\(\frac{{{B'}{C'}}}{{BC}} = \frac{{AC}}{{{A'}{C'}}}.\)
Câu 6 :
Cho \(\Delta MNP \backsim \Delta KIH\) , biết \(\hat M = \hat K,MN = 2cm,MP = 8cm,KH = 4cm\) , thì KI bằng bao nhiêu:
-
A.
\(KI = 2cm.\)
-
B.
\(KI = 6cm.\)
-
C.
\(KI = 4cm.\)
-
D.
\(KI = 1cm.\)
Câu 7 :
Cho \(\Delta ABC\) , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) Kết luận nào sau đây sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ABC.}\)
Câu 8 :
Cho \(\Delta ABC\) , có AC = 18cm; AB = 9cm; BC = 15cm. Trên cạnh AC lấy điểm N sao cho AN = 3cm, trên cạnh AB lấy điểm M sao cho AM = 6cm. Tính độ dài đoạn thẳng MN:
-
A.
MN= 6cm
-
B.
MN = 5cm
-
C.
MN = 8cm
-
D.
MN = 9cm
-
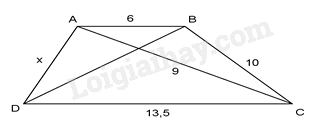
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Câu 10 :
Cho hình thang vuông \(ABCD(\hat A = \hat D = {90^0})\) có AB = 16cm, CD = 25cm,
BD = 20cm. Độ dài cạnh BC là:
-
A.
10 cm
-
B.
12cm
-
C.
15cm
-
D.
9cm
Câu 11 :
Cho \(\Delta MNP \backsim \Delta EFH\) theo tỉ số k. Gọi \(M{M'},E{E'}\) lần lượt là hai trung tuyến của \(\Delta MNP\) và \(\Delta EFH\) . Khi đó ta chứng minh được:
-
A.
\(\frac{{E{E'}}}{{M{M'}}} = k\)
-
B.
\(\frac{{M{M '}}}{{E{E '}}} = k\)
-
C.
\(\frac{{M{M '}}}{{E{E '}}} = {k^2}\)
-
D.
\(\frac{{E{E '}}}{{M{M '}}} = {k^2}\)
Câu 12 :
Cho tam giác nhọn ABC có \(\hat C = {60^0}\) . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
-
A.
\({30^0}\)
-
B.
\({60^0}\)
-
C.
\({45^0}\)
-
D.
\({50^0}\)
Câu 13 :
Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc B bằng bao nhiêu lần góc A?
-
A.
\(\hat B = \frac{{\hat A}}{3}\)
-
B.
\(\hat B = \frac{2}{3}\hat A\)
-
C.
\(\hat B = \frac{{\hat A}}{2}\)
-
D.
\(\hat B = \hat A\)
Câu 14 :
Cho hình thoi ABCD cạnh a, có \(\hat A = {60^0}\) . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính \(\widehat {BKD}\) .
-
A.
\(\widehat {BKD} = {60^0}\)
-
B.
\(\widehat {BKD} = {100^0}\)
-
C.
\(\widehat {BKD} = {120^0}\)
-
D.
\(\widehat {BKD} = {115^0}\)
CÁC BÀI TẬP KHÁC
