Giải câu hỏi trang 55, 56, 57 SGK Toán 7 tập 1 - Kết nối tri thức

Vẽ hình và viết giả thiết, kết luận của định lí: “ Hai góc đối đỉnh thì bằng nhau”...Em hãy chứng minh định lí: “ Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”

Tổng hợp đề thi giữa kì 1 lớp 7 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Lựa chọn câu để xem lời giải nhanh hơn

Luyện tập 1

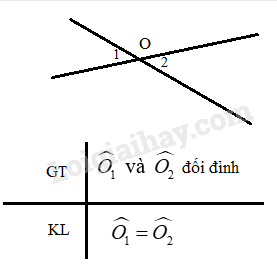
Vẽ hình và viết giả thiết, kết luận của định lí:

“ Hai góc đối đỉnh thì bằng nhau”

Phương pháp giải:

Vẽ hình

Giả thiết là điều đề bài cho

Kết luận là điều cần chứng minh

Lời giải chi tiết:

Luyện tập 2

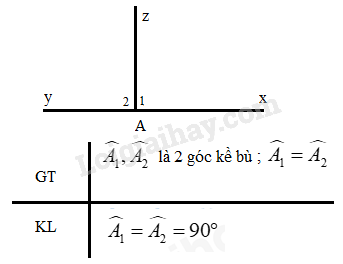
Em hãy chứng minh định lí: “ Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”

Phương pháp giải:

Vẽ hình, viết giả thiết, kết luận rồi chứng minh

Lời giải chi tiết:

Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù)

Mà \(\widehat {{A_1}} = \widehat {A_2^{}}\)

\(\begin{array}{l} \Rightarrow \widehat {{A_1}} + \widehat {{A_1}} = 180^\circ \\ \Rightarrow 2.\widehat {{A_1}} = 180^\circ \\ \Rightarrow \widehat {{A_1}} = 180^\circ :2 = 90^\circ \end{array}\)

Vậy \(\widehat {{A_1}} = \widehat {A{}_2} = 90^\circ \) (đpcm)

Tranh luận

Em có ý kiến gì về hai ý kiến trên?

Phương pháp giải:

Chỉ ra ví dụ chứng tỏ khẳng định không đúng.

Lời giải chi tiết:

Em thấy bạn Vuông nói đúng

Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.

Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 23 phiếu

Bài tiếp theo

Giải bài 3.24 trang 57 SGK Toán 7 tập 1 - Kết nối tri thức
Có thể coi định lí: “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Giải bài 3.25 trang 57 SGK Toán 7 tập 1 - Kết nối tri thức
Hãy chứng minh định lí nói ở Ví dụ trang 56: “ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó, ta đã sử dụng những điều đúng đã biết nào?
Giải bài 3.26 trang 57 SGK Toán 7 tập 1 - Kết nối tri thức
Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây là đúng?
Lý thuyết Định lí và chứng minh định lí SGK Toán 7 - Kết nối tri thức
1. Định lí. Giả thiết, kết luận của định lí