Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng- ..

Giải bài 4.50 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống


Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tuỳ ý trên đường thẳng AH sao cho M không trùng với A(H.4.54). Chứng minh rằng:

Đề bài

Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tuỳ ý trên đường thẳng AH sao cho M không trùng với A(H.4.54). Chứng minh rằng: \(\widehat {MBA} = \widehat {MCA}\).

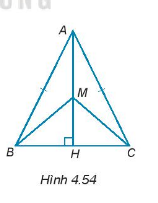
Phương pháp giải - Xem chi tiết

- Chứng minh: \(\Delta HAB = \Delta HAC\left( {ch - cgv} \right)\)

- Chứng minh:\(\Delta MBA = \Delta MCA\left( {c - g - c} \right)\)

Lời giải chi tiết

Xét \(\Delta HAB\) và \(\Delta HAC\) có:

\(\widehat {AHB} = \widehat {AHC} = {90^0}\)

AB = AC

AH: Cạnh chung

\( \Rightarrow \Delta HAB = \Delta HAC\left( {ch - cgv} \right)\)

\( \Rightarrow \widehat{HAB}=\widehat{HAC}\) (2 góc tương ứng)

Xét \(\Delta MBA\) và \(\Delta MCA\) có:

AB = AC

\(\widehat {MAB} = \widehat {MAC}\)

AM: Cạnh chung

\( \Rightarrow \Delta MBA = \Delta MCA\left( {c - g - c} \right)\)

\(\Rightarrow \widehat {MBA} = \widehat {MCA}\) (2 góc tương ứng)


Bình chọn:
4.3 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store