-
Chương 1: Số hữu tỉ - SBT KNTT
-
Chương 2: Số thực - SBT KNTT
-
Chương 3: Góc và đường thẳng song song - SBT KNTT
-
Chương 4: Tam giác bằng nhau - SBT KNTT
-
Chương 5: Thu thập và biểu diễn dữ liệu - SBT KNTT
-
Chương 6. Tỉ lệ thức và đại lượng tỉ lệ - SBT KNTT
-
Chương 7. Biểu thức đại số và đa thức một biến - SBT KNTT
-
Chương 8. Làm quen với biến cố và xác suất của biến cố
-
Chương 9. Quan hệ giữa các yếu tố trong một tam giác - SBT KNTT
-
Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam giác
-
Bài 32. Quan hệ giữa đường vuông góc và đường xiên
-
Bài 33. Quan hệ giữa ba cạnh của tam giác
-
Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
-
Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
-
Ôn tập chương 9
-
-
Chương 10. Một số hình khối trong thực tiễn - SBT KNTT
-
Bài tập cuối năm
Giải bài 4.47 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABH vuông tại đỉnh H có
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
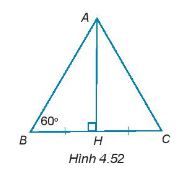
Đề bài
Cho tam giác ABH vuông tại đỉnh H có \(\widehat {ABH} = {60^0}\). Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng \(\Delta ABC\) là tam giác đều và \(BH = \dfrac{{AB}}{2}\)
Phương pháp giải - Xem chi tiết
-Chứng minh: \(\Delta HAB = \Delta HAC\left( {c - g - c} \right)\)
-Chứng minh: Tam giác ABC đều (tam giác cân có 1 góc bằng 60 độ).
Lời giải chi tiết
Xét \(\Delta HAB\) và \(\Delta HAC\) có:
\(\widehat {AHB} = \widehat {AHC} = {90^0}\\HB = HC\\HA:Chung\\ \Rightarrow \Delta HAB = \Delta HAC\left( {c - g - c} \right)\)
\(\Rightarrow AB = AC\) (2 cạnh tương ứng)
\(\Rightarrow \Delta ABC\) cân tại A
\(\Rightarrow \widehat{B}=\widehat{C}\)
Mặt khác, theo định lí tổng 3 góc trong một tam giác, ta có: \(\widehat A = {180^0} - \widehat B - \widehat C = {180^0} - 2\widehat B = 180^0-2.60^0={60^0}\)
Ta được:\(\widehat{A}=\widehat{B} (=60^0)\)
\(\Rightarrow \Delta ABC\) cân tại đỉnh C nên CA = CB
\( \Rightarrow AB = BC = CA\)
\( \Rightarrow \Delta ABC\) là tam giác đều
\( \Rightarrow BH = \dfrac{{BC}}{2} = \dfrac{{AB}}{2}\)
Bình luận
Chia sẻ
- Giải bài 4.48 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.49 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.50 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.46 trang 69 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 4.45 trang 69 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải Bài 18 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 17 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 16 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 15 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 14 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 18 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 17 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 16 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 15 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 14 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
