-
GIẢI SGK TOÁN 8 CÁNH DIỀU - MỚI NHẤT
-
Toán 7 tập 1 - Cánh diều
-
Chương I. Số hữu tỉ
-
Chương II. Số thực
- Bài 1. Số vô tỉ. Căn bậc hai số học
- Bài 2. Tập hợp R các số thực
- Bài 3. Giá trị tuyệt đối của một số thực
- Bài 4. Làm tròn và ước lượng
- Bài 5. Tỉ lệ thức
- Bài 6. Dãy tỉ số bằng nhau
- Bài 7. Đại lượng tỉ lệ thuận
- Bài 8. Đại lượng tỉ lệ nghịch
- Bài tập cuối chương II
- Hoạt động thực hành và trải nghiệm. Chủ đề 1: Một số hình thức khuyến mãi trong kinh doanh
-
Chương III. Hình học trực quan
-
Chương IV. Góc. Đường thẳng song song
-
-
Toán 7 tập 2 - Cánh diều
-
Chương V. Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập, phân loại và biểu diễn dữ liệu
- Bài 2. Phân tích và xử lí dữ liệu
- Bài 3. Biểu đồ đoạn thẳng
- Bài 4. Biểu đồ hình quạt tròn
- Bài 5. Biến cố trong một số trò chơi đơn giản
- Bài 6. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài tập cuối chương V
- Hoạt động thực hành và trải nghiệm. Chủ đề 3. Dung tích phổi
-
Chương VI. Biểu thức đại số
-
Chương VII. Tam giác
- Bài 1. Tổng các góc của một tam giác
- Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
- Bài 3. Hai tam giác bằng nhau
- Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
- Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
- Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc
- Bài 7. Tam giác cân
- Bài 8. Đường vuông góc và đường xiên
- Bài 9. Đường trung trực của một đoạn thẳng
- Bài 10. Tính chất ba đường trung tuyến của tam giác
- Bài 11. Tính chất ba đường phân giác của tam giác
- Bài 12. Tính chất ba đường trung trực của tam giác
- Bài 13. Tính chất ba đường cao của tam giác
- Bài tập cuối chương VII
-
Giải bài 3 trang 92 SGK Toán 7 tập 2 - Cánh diều
Cho Hình 66 có
Đề bài
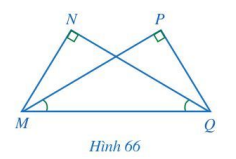
Cho Hình 66 có \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\). Chứng minh MN = QP, MP = QN.
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác MNQ bằng tam giác QPM.
Lời giải chi tiết
Ta có: tổng ba góc trong một tam giác bằng 180° và \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\) nên \(\widehat {PQM} = \widehat {NMQ}\).
Xét hai tam giác MNQ và QPM có:
\(\widehat {NQM}=\widehat {PMQ}\)
MQ chung
\(\widehat {NMQ}=\widehat {PQM}\)
Vậy \(\Delta MNQ = \Delta QPM\)(g.c.g). Do đó MN = QP, MP = QN ( 2 cạnh tương ứng)
Bình luận
Chia sẻ
- Giải bài 4 trang 92 SGK Toán 7 tập 2 - Cánh diều
- Giải bài 5 trang 92 SGK Toán 7 tập 2 - Cánh diều
- Giải bài 6 trang 92 SGK Toán 7 tập 2 - Cánh diều
- Giải bài 2 trang 91 SGK Toán 7 tập 2 - Cánh diều
- Giải bài 1 trang 91 SGK Toán 7 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Tạo đồ dùng dạng hình lăng trụ đứng SGK Toán 7 Cánh diều tập 1
- Giải câu hỏi trang 39, 40 SGK Toán 7 Cánh diều tập 2
- Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều
- Tạo đồ dùng dạng hình lăng trụ đứng SGK Toán 7 Cánh diều tập 1
- Giải câu hỏi trang 39, 40 SGK Toán 7 Cánh diều tập 2
- Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều
