 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 III. Một số đề kiểm tra
III. Một số đề kiểm tra
Câu 1 Đề III trang 133 SGK Hình học 12 Nâng cao
Câu 1. Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB và là mặt phẳng đi qua ba điểm D, N, B’. a) Mặt phẳng cắt hình hộp đã cho theo thiết diện là hình gì? b) Chứng minh rằng mặt phẳng phân chia khối hộp đã cho thành hai khối đa diện và bằng nhau. c) Tính tỉ số thể tích của khối đa diện và thể tích của khối tứ diện AA’BD.
Câu 1. Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB và \(\left( \alpha \right)\) là mặt phẳng đi qua ba điểm D, N, B’.
LG a
Mặt phẳng \(\left( \alpha \right)\) cắt hình hộp đã cho theo thiết diện là hình gì?
Lời giải chi tiết:
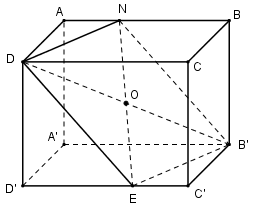
Giả sử \(\left( \alpha \right) \cap C'D' = E\) thì thiết diện của hình hộp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác DNB’E.
Ta có:
\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {ABCD} \right) = DN \hfill \cr
\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = B'E \hfill \cr
\left( {ABCD} \right)\parallel \left( {A'B'C'D'} \right) \hfill \cr} \right. \Rightarrow DN\parallel B'E.\)
Tương tự ta có:
\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {AA'B'B} \right) = {NB'} \hfill \cr
\left( \alpha \right) \cap \left( {CC'D'D} \right) = DE \hfill \cr
\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right) \hfill \cr} \right. \Rightarrow NB'\parallel DE.\)
Xét tứ giác DNB’E có: DN // B’E, NB’ // DE.
Vậy DNB’E là hình bình hành.
LG b
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) phân chia khối hộp đã cho thành hai khối đa diện \({H_1}\) và \({H_2}\) bằng nhau.
Lời giải chi tiết:
\(mp\left( \alpha \right)\) chia khối hộp thành hai khối đa diện \({H_1}:ADNA'B'ED'\) và \({H_2}:C'B'ECDNB.\)
Gọi O là giao điểm hai đường chéo B’D và NE của hình bình hành DNB’E suy ra O là trung điểm của B’D. Do đó O là tâm hình hộp ABCD.A’B’C’D’.
Gọi \({D_{(O)}}\) là phép đối xứng qua tâm O ta có:
\({D_{(O)}}\): \(A \to C'\)
\(\eqalign{
& N \to E \cr
& B' \to D \cr
& E \to N \cr
& D' \to B \cr
& A' \to C \cr
& D \to B' \cr} \)
\( \Rightarrow \)\({D_{(O)}}\): \(ADNA'B'ED' \to C'B'ECDNB\) hay \({D_{(O)}}\): \({H_1} \to {H_2}.\)
Mà phép đối xứng tâm O là phép dời hình nên \({V_{{H_1}}} = {V_{{H_2}}}.\)
LG c
Tính tỉ số thể tích của khối đa diện \({H_1}\) và thể tích của khối tứ diện AA’BD.
Lời giải chi tiết:
Gọi \({V_{ABCD.A'B'C'D'}} = V.\)
Ta có: \({V_{AA'BD}} = {V_{A'.ABD}}.\)
\({S_{\Delta ABD}} = {1 \over 2}{S_{ABCD}} \)
\(\Rightarrow {V_{A'.ABD}} = {1 \over 3}AA'.{S_{\Delta ABD}} \)\(= {1 \over 3}.AA'.{1 \over 2}{S_{ABCD}} = {1 \over 6}{V_{ABCD.A'B'C'D'}} = {V \over 6}.\)
Mà \({V_{{H_1}}} = {V_{{H_2}}} = {V \over 2}.\)
Suy ra \({{{V_{{H_1}}}} \over {{V_{AA'BD}}}} = {{{V \over 2}} \over {{V \over 6}}} = 3.\)
Loigiaihay.com












Danh sách bình luận