 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 III. Một số đề kiểm tra
III. Một số đề kiểm tra
Câu 1 Đề I trang 132 SGK Hình học 12 Nâng cao
Câu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a va cạnh bên bằng . a) Tính thể tích của hình chóp đã cho. b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. c) Gọi A’ và C’ lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hai hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a va cạnh bên bằng \(a\sqrt 2 \).
LG a
Tính thể tích của hình chóp đã cho.
Lời giải chi tiết:
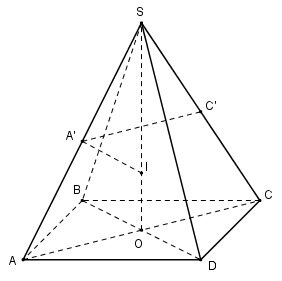
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right).\)
Ta có ABCD là hình vuông cạnh a nên \(AC = BD = a\sqrt 2 \Rightarrow AO = {{a\sqrt 2 } \over 2}.\)
Xét tam giác vuông SOA có: \(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {2{a^2} - {{{a^2}} \over 2}} = {{a\sqrt 6 } \over 2}.\)
\(\eqalign{
& {S_{ABCD}} = {a^2} \cr
& \Rightarrow {V_{S.ABCD}} = {1 \over 3}SO.{S_{ABCD}} = {1 \over 3}{{a\sqrt 6 } \over 2}.{a^2} = {{{a^3}\sqrt 6 } \over 6}. \cr} \)
LG b
Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
Lời giải chi tiết:
Gọi A’ là trung điểm của SA.
Trong (SAC) qua A’ kẻ đường thẳng vuông góc với SA cắt SO tại I.
Suy ra I là tâm mặt cầu ngoại tiếp chóp S.ABCD.
Dễ thấy
\(\eqalign{
& \Delta SA'I\,\,\text{ đồng dạng }\,\,\Delta SOA\,(g.g) \cr
& \Rightarrow {{SA} \over {SI}} = {{SO} \over {SA'}} \Rightarrow SI = {{SA.SA'} \over {SO}} = {{a\sqrt 2 .{{a\sqrt 2 } \over 2}} \over {{{a\sqrt 6 } \over 2}}} = {{a\sqrt 6 } \over 3} = R \cr} \)
LG c
Gọi A’ và C’ lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hai hình chóp A’.ABCD và C’.CBAD bằng nhau.
Lời giải chi tiết:
Ta có A’C’ // (ABCD) \( \Rightarrow d\left( {A';\left( {ABCD} \right)} \right) = d\left( {C';\left( {ABCD} \right)} \right)\)
\( \Rightarrow {V_{A'.ABCD}} = {V_{C'.CBAD}}.\)
Vậy hai khối chóp A’.ABCD và C’.CBAD bằng nhau.
Loigiaihay.com












Danh sách bình luận