Câu 6 trang 91 SGK Hình học 11 Nâng cao

Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.

Đề bài

Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.

Lời giải chi tiết

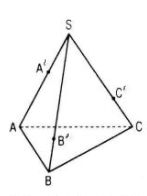
Ta có: \(\overrightarrow {SA} = a\overrightarrow {SA'} ,\;\overrightarrow {SB} = b\overrightarrow {SB'} ,\;\overrightarrow {SC} = c\overrightarrow {SC} .\)

Gọi G là trọng tâm của tam giác ABC thì

\(\eqalign{ & \overrightarrow {SG} = {1 \over 3}.\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) \cr & Vay\,\overrightarrow {SG} = {a \over 3}\overrightarrow {SA'} + {b \over 3}\overrightarrow {SB'} + {c \over 3}\overrightarrow {SC'} \cr} \)

Mặt phẳng (A’B’C’) đi qua G khi và chỉ khi 4 điểm G, A’, B’, C’ đồng phẳng, nên theo kết quả bài tập 5 (SGK trang 91) , điều đó xảy ra nếu và chỉ nếu \({a \over 3} + {b \over 3} + {c \over 3} = 1\) , tức là: a + b + c = 3.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 8 phiếu

Bài tiếp theo

Câu 5 trang 91 SGK Hình học 11 Nâng cao
Trong không gian cho tam giác ABC.
Câu 4 trang 91 SGK Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Câu 3 trang 91 SGK Hình học 11 Nâng cao
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.
Câu 2 trang 91 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD.
Câu 1 trang 91 SGK Hình học 11 Nâng cao
Ba vecto có đồng phẳng không nếu một trong hai điều sau đây xảy ra ?