Bài 4: Hai mặt phẳng song song

Câu 33 trang 68 SGK Hình học 11 Nâng cao

Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành

Đề bài

Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành

Phương pháp giải - Xem chi tiết

- Chứng minh (a,d)//(b,c), sử dụng: "Mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P)//(Q)".

- Chứng minh A'D'//B'C' dựa vào định lí: "Nếu hai mặt phẳng (P) và (Q) song song thì mọi mặt phẳng (R) đã cắt (P) thì sẽ cắt (Q) và các giao tuyến của chúng song song."

Lời giải chi tiết

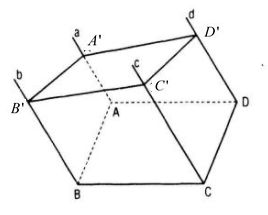
Ta có:

\(\begin{array}{l}
\left\{ \begin{array}{l}
a//b\\
b \subset \left( {b,c} \right)
\end{array} \right. \Rightarrow a//\left( {b,c} \right)\\
\left\{ \begin{array}{l}
AD//BC\\
BC \subset \left( {b,c} \right)
\end{array} \right. \Rightarrow AD//\left( {b,c} \right)
\end{array}\)

Mà \(a \cap AD = A\) và \(a,AD \subset \left( {a,d} \right)\) nên (a,d)//(b,c).

Vì hai mặt phẳng (a, d) và (b, c) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này lần lượt theo hai giao tuyến A’D’ và B'C’ song song với nhau.

Lại có:

\(\begin{array}{l}
\left\{ \begin{array}{l}
a//d\\
d \subset \left( {c,d} \right)
\end{array} \right. \Rightarrow a//\left( {c,d} \right)\\
\left\{ \begin{array}{l}
AB//CD\\
CD \subset \left( {c,d} \right)
\end{array} \right. \Rightarrow AB//\left( {c,d} \right)
\end{array}\)

Mà \(a \cap AB = A\) và \(a,AB \subset \left( {a,b} \right)\) nên (a,b)//(c,d).

Vì hai mặt phẳng (a,b) và (c,d) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này lần lượt theo hai giao tuyến A’B’ và C'D’ song song với nhau.

Vậy A’B’C’D’ là hình bình hành.

Loigiaihay.com