Câu 31 trang 68 SGK Hình học 11 Nâng cao

Cho hai đường thẳng chéo nhau. Chứng minh rằng có đúng hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng đó

Đề bài

Cho hai đường thẳng chéo nhau. Chứng minh rằng có đúng hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng đó

Quảng cáo

Lời giải chi tiết

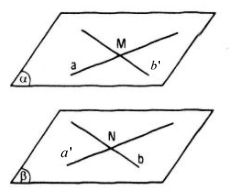
Gọi hai đường thẳng chéo nhau là a và b.

Trên đường thẳng a, ta lấy điểm M, qua M kẻ đường thẳng b’ // b

Trên đường thẳng b, ta lấy điểm N, qua N ta kẻ đường thẳng a’ // a

Gọi (α) = mp(a, b’), (β) = mp(b, a’) thì (α) // (β)

* Ta chứng tỏ cặp mặt phẳng (α), (β) là duy nhất.

Thật vậy, giả sử tồn tại cặp (α’) , (β’) sao cho (α’) chứa a, (β’) chứa b và $(α’) // (β’)$ . Ta chứng minh $(α’) ≡ (α)$ và $(β’) ≡ (β)$ .

- Do (α’) và (α) cùng chứa a, nên nếu (α’) và (α) không trùng nhau thì $(α’) ∩ (α) = a$ (1)

- Do $(α’) // (β’) ⇒ b // (α’)$ (2)

- Do $(α) // (β) ⇒ b // (α)$ (3)

Từ (1), (2) và (3) suy ra a // b, mâu thuẫn giả thiết

Vậy $(α) ≡ (α’)$ , tương tự $(β) ≡ (β’)$

Do đó cặp mặt phẳng $(α), (β)$ duy nhất.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

2.9 trên 8 phiếu

Bài tiếp theo

Câu 32 trang 68 SGK Hình học 11 Nâng cao
Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b
Câu 33 trang 68 SGK Hình học 11 Nâng cao
Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành
Câu 34 trang 68 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Gọi M là trung điểm của AB. Hỏi mặt phẳng (P) qua điểm M, song song với cả AD và BC có đi qua trung điểm N của CD không ? Tại sao ?
Câu 35 trang 68 SGK Hình học 11 Nâng cao
Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho ({{IM} over {IN}} = k,k ne 0)cho trước
Câu 36 trang 68 SGK Hình học 11 Nâng cao
Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.
Câu 37 trang 68 SGK Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng a. mp(BDA’) // mp(B’D’C) b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
Câu 38 trang 68 SGK Hình học 11 Nâng cao
Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
Câu 39 trang 68 SGK Hình học 11 Nâng cao
Cho hình chóp cụt ABC.A’B’C’ có đáy lớn ABC và các cạnh bên AA’, BB’, CC’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và M’, N’, P’ lần lượt là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt
Câu 30 trang 67 SGK Hình học 11 Nâng cao
a. Hình hộp là một hình lăng trụ
Câu 29 trang 67 SGK Hình học 11 Nâng cao
a. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.