Bài 9 trang 177 SGK Đại số 10 Nâng cao

Có 100 học sinh tham dự kỳ thi học sinh giỏi Toán (thang điểm là 20) kết quả được cho bởi bảng sau.

Lựa chọn câu để xem lời giải nhanh hơn

Có 100 học sinh tham dự kỳ thi học sinh giỏi Toán (thang điểm là 20) kết quả được cho bởi bảng sau.

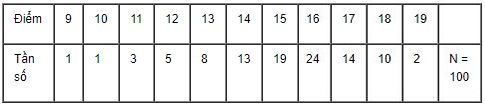
LG a

Tính số trung bình.

Lời giải chi tiết:

Số trung bình:

\(\eqalign{
& \overline x = {1 \over {100}}(9.1 + 10.1 + 11.3 + 12.5 + 13.8 + 14.13\cr&\;\;\;\;\; + 15.19 + 16.24 + 17.14 + 18.10 + 19.2) \cr
& = 15,23 \cr} \)

LG b

Tính số trung vị và mốt. Nêu ý nghĩa

Lời giải chi tiết:

Ta có:

\(\left\{ \matrix{
{N \over 2} = 50 \hfill \cr
{N \over 2} + 1 = 51 \hfill \cr} \right.\)

Số liệu đứng thứ 50 là 15 và số liệu đứng thứ 51 là 16 nên số trung vị là:

\({1 \over 2}(15 + 16) = 15,5\)

Mốt là 16.

Ý nghĩa: Có khoảng một nửa số sinh viên có điểm dưới 15,5 và số học sinh đạt điểm 16 là nhiều nhất.

LG c

Tính phương sai và độ lệch chuẩn

Lời giải chi tiết:

Phương sai:

Sử dụng máy tính ta có:

\(\eqalign{
& {s^2} = {1 \over {100}}(\sum\limits_{i = 1}^{11} {{n_i}x_i^2} ) - {1 \over {{{100}^2}}}{(\sum\limits_{i = 1}^{11} {{n_i}x_i} )^2} \approx 3,96 \cr
& s \approx 1,99 \cr} \)

Cách khác:

\(\begin{array}{l}
{s^2} = \frac{1}{{100}}[1.{(9 - 15,23)^2} + 1.{(10 - 15,23)^2}\\
+ 3.{(11 - 15,23)^2} + 5.{(12 - 15,23)^2} + ...\\
+ 10.{(18 - 15,23)^2} + 2.{\left( {19 - 15,23} \right)^2}\\
= 3,96\\
\Rightarrow s = 1,99
\end{array}\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4 trên 8 phiếu

Bài tiếp theo

Bài 10 trang 178 SGK Đại số 10 Nâng cao
Tính khối lượng trung bình của một của khoai tây. Tính phương sai và độ lệch chuẩn.
Bài 11 trang 178 SGK Đại số 10 Nâng cao
Bảng sau đây trích từ số theo dõi bán hàng của một cửa hàng bán xa máy:
Bài 12 trang 178 SGK Đại số 10 Nâng cao
Số liệu sau đây cho ta lãi (quy tròn) hàng tháng của một cửa hàng trong năm 2000. Đơn vị là triệu đồng.
Bài 13 trang 178 SGK Đại số 10 Nâng cao
Một cửa hàng vật liệu xây dựng thống kê số bao xi măng bán ra trong 23 ngày cuối nắm 2004. Kết quả như sau:
Bài 14 trang 179 SGK Đại số 10 Nâng cao
Số lượng khách đến thăm quan một địa điểm du lịch trong mỗi tháng được thống kê như sau:
Bài 15 trang 179 SGK Đại số 10 Nâng cao
Trên hai con đường A và B trạm kiểm soát đã ghi lại tốc độ (km/h) của 30 chiếc ôto trên mỗi con đường như sau: