-
Toán 11 tập 1 - Kết nối tri thức với cuộc sống
-
Giải Toán 11 tập 2 - Kết nối tri thức với cuộc sống
Bài 35 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức
Cho hình chóp (S.ABCD) có đáy ABCD là hình chữ nhật, (AD = a,AB = asqrt 2 ).
Đã có lời giải SGK Toán lớp 12 - Kết nối tri thức (mới)
Đầy đủ - Chi tiết - Chính xác
Đề bài
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật, \(AD = a,AB = a\sqrt 2 \). Biết \(SA \bot (ABCD)\) và \(SA = a\sqrt 3 \). Gọi \(M\) là trung điểm của cạnh CD.
a) Chứng minh rằng \(BD \bot (SAM)\).
b) Tính theo a thể tích khối chóp S.ABMD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thể tích khối chóp \(V = \frac{1}{3}h.S\)
Lời giải chi tiết
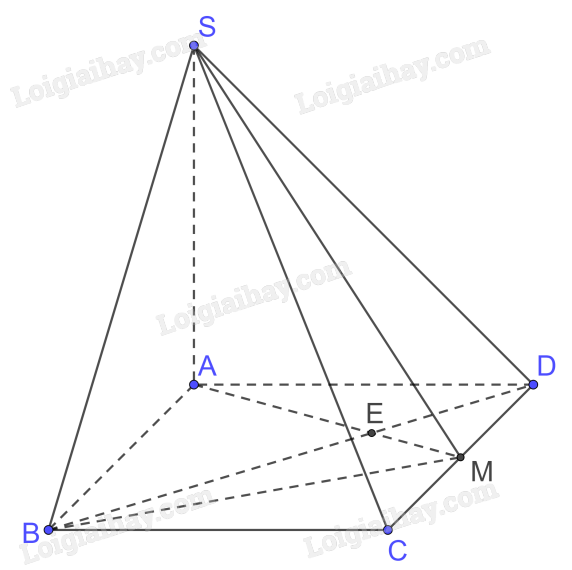
a) Xét tam giác ABD vuông tại A có \(\tan \widehat {ADB} = \frac{{AB}}{{AD}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 \)
Xét tam giác ADM vuông tại D có \(\tan \widehat {AMD} = \frac{{AD}}{{DM}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \)
Do đó \(\widehat {ADB} = \widehat {AMD}\)
Mà \(\widehat {ADB} + \widehat {EDM} = {90^0}\) nên \(\widehat {AMD} + \widehat {EDM} = {90^0} \Rightarrow \widehat {DEM} = {90^0} \Rightarrow AM \bot BD\)
Ta có \(AM \bot BD,SA \bot BD \Rightarrow BD \bot \left( {SAM} \right)\)
b) Vì tứ giác ABMD là hình thang vuông nên
\({S_{ABMD}} = \frac{{\left( {DM + AB} \right)AD}}{2} = \frac{{\left( {\frac{{a\sqrt 2 }}{2} + a\sqrt 2 } \right)a}}{2} = \frac{{3{a^2}\sqrt 2 }}{4}\)
Vậy thể tích khối chóp S.ABMD là \(V = \frac{1}{3}SA.{S_{ABMD}} = \frac{1}{3}.a\sqrt 3 .\frac{{3{a^2}\sqrt 2 }}{4} = \frac{{{a^3}\sqrt 6 }}{4}\)
Bình luận
Chia sẻ
- Bài 36 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 37 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 38 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 34 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 33 trang 109 SGK Toán 11 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Lý thuyết Đạo hàm cấp hai - Toán 11 Kết nối trí thức
- Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối trí thức
- Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối trí thức
- Lý thuyết Công thức nhân xác suất cho hai biến cố độc lập - Toán 11 Kết nối trí thức
- Lý thuyết Công thức cộng xác suất - Toán 11 Kết nối trí thức
- Lý thuyết Đạo hàm cấp hai - Toán 11 Kết nối trí thức
- Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối trí thức
- Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối trí thức
- Lý thuyết Công thức nhân xác suất cho hai biến cố độc lập - Toán 11 Kết nối trí thức
- Lý thuyết Công thức cộng xác suất - Toán 11 Kết nối trí thức
