-
Toán 11 tập 1 - Kết nối tri thức với cuộc sống
-
Giải Toán 11 tập 2 - Kết nối tri thức với cuộc sống
Bài 15 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
Cho hình lập phương (ABCD.A'B'C'D') có (AC' = sqrt 3 ). Khoảng cách giữa hai đường thẳng (AB') và (BC') bằng
Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AC' = \sqrt 3 \). Khoảng cách giữa hai đường thẳng \(AB'\) và \(BC'\) bằng
A. \(\frac{1}{3}\).
B. \(\frac{{\sqrt 3 }}{3}\).
C. \(\frac{{\sqrt 3 }}{2}\).
D. \(\frac{1}{2}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này đến mặt phẳng song song chứa đường thẳng kia
Quảng cáo
Lời giải chi tiết
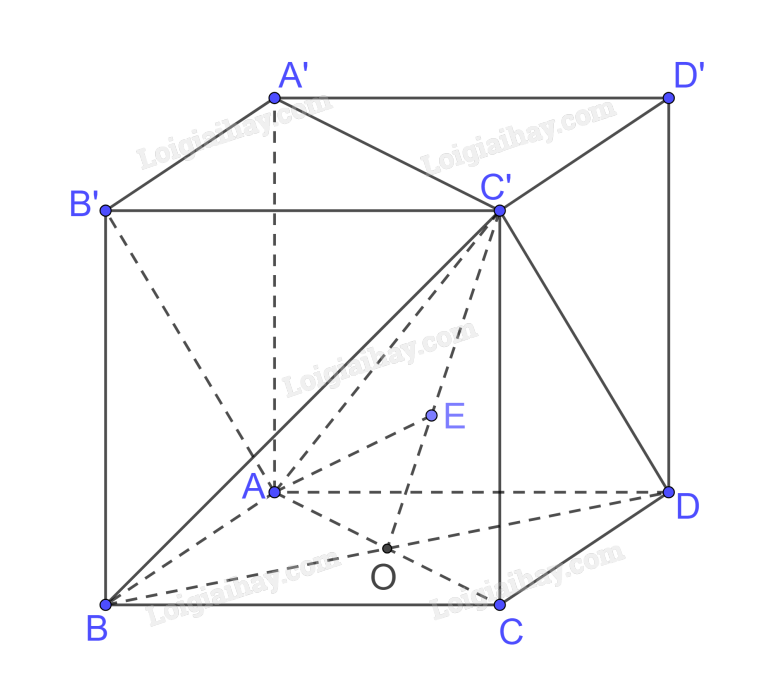
Gọi AC giao BD tại O
Ta có \(AC \bot BD,BD \bot AA' \Rightarrow BD \bot \left( {ACC'A'} \right);BD \subset \left( {BDC'} \right) \Rightarrow \left( {ACC'A'} \right) \bot \left( {BDC'} \right)\)
Mà \(\left( {ACC'A'} \right) \cap \left( {BDC'} \right) = OC'\)
Trong (ACCA’) kẻ \(AE \bot OC'\)
Do đó \(AE \bot \left( {BDC'} \right)\)
Ta có AB’ // DC’ nên \(d\left( {AB',BC'} \right) = d\left( {AB',\left( {BDC'} \right)} \right) = d\left( {A,\left( {BDC'} \right)} \right) = AE\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {2A{B^2}} = AB\sqrt 2 \)
Xét tam giác ACC’ vuông tại C có
\(\begin{array}{l}A{C^2} + C{{C'}^2} = A{{C'}^2}\\ \Leftrightarrow {\left( {AB\sqrt 2 } \right)^2} + A{B^2} = 3\\ \Leftrightarrow 3A{B^2} = 3\\ \Leftrightarrow AB = 1\\ \Leftrightarrow AC = \sqrt 2 \end{array}\)
Xét tam giác OCC’ vuông tại C có \(C'O = \sqrt {C{{C'}^2} + O{C^2}} = \sqrt {{1^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = \frac{{\sqrt 6 }}{2}\)
Dễ dàng chứng minh
\( \Rightarrow \frac{{AE}}{{CC'}} = \frac{{AO}}{{C'O}} \Rightarrow AE = \frac{{AO.CC'}}{{C'O}} = \frac{{\frac{{\sqrt 2 }}{2}.1}}{{\frac{{\sqrt 6 }}{2}}} = \frac{{\sqrt 3 }}{3}\)
Đáp án B
Bình luận
Chia sẻ
- Bài 16 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 17 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 18 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 19 trang 107 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 20 trang 107 SGK Toán 11 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Đạo hàm cấp hai - Toán 11 Kết nối tri thức
- Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Công thức nhân xác suất cho hai biến cố độc lập - Toán 11 Kết nối tri thức
- Lý thuyết Công thức cộng xác suất - Toán 11 Kết nối tri thức
- Lý thuyết Đạo hàm cấp hai - Toán 11 Kết nối tri thức
- Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Định nghĩa và ý nghĩa của đạo hàm - Toán 11 Kết nối tri thức
- Lý thuyết Công thức nhân xác suất cho hai biến cố độc lập - Toán 11 Kết nối tri thức
- Lý thuyết Công thức cộng xác suất - Toán 11 Kết nối tri thức
