Bài 15 trang 53 SGK Hình học 12 Nâng cao

Mặt phẳng đi qua trục của một hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh 2R.

Đề bài

Mặt phẳng đi qua trục của một hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh \(2R\).

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích của khối trụ.

c) Tính thể tích của khối lăng trụ tứ giác đều nội tiếp hình trụ.

Lời giải chi tiết

Mặt phẳng đi qua \(OO’\) của hình trụ, cắt hình trụ theo thiết diện là hình vuông \(ABCD\) cạnh \(2R\), do đó bán kính đáy bằng \(R\) và đường sinh \(AD = 2R\).

a) Ta có:

\(\eqalign{
& {S_{xq}} = 2\pi .R.2R = 4\pi {R^2} \cr
& {S_{tp}} = {S_{xq}} + 2{S_{day}} \cr &= 4\pi {R^2} + 2\pi {R^2} = 6\pi {R^2} \cr} \)

b) Thể tích của khối trụ là \(V = \pi {R^2}.2R = 2\pi {R^3}\).

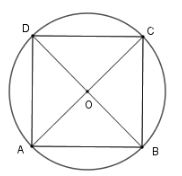
c) Hình lăng trụ tứ giác đều nội tiếp hình trụ cạnh bên bằng \(2R\)

Đáy lăng trụ là hình vuông có đường chéo AC=BD=2R như hình vẽ.

Khi đó OA=OB=R nên \(AB=R\sqrt 2 \)

Thể tích lăng trụ tứ giác đều là \({V_{LT}} = (R\sqrt 2)^2.2R = 4{R^3}\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 8 phiếu

Bài tiếp theo

Bài 16 trang 54 SGK Hình học 12 Nâng cao
Một hình trụ có bán kính đáy bằng R và chiều cao . a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ. b) Tình thể tích của khối trụ giới hạn bởi hình trụ.
Bài 14 trang 53 SGK Hình học 12 Nâng cao
Chứng minh rằng các tiếp tuyến của mặt cầu song song với một đường thẳng cố định luôn nằm trên một mặt trụ xác định.
Bài 13 trang 53 SGK Hình học 12 Nâng cao
Cho đường tròn (O;R) nằm trong mặt phẳng (P). Tìm tập hợp các điểm M trong không gian sao cho hình chiếu của chúng trên (P) luôn nằm trên đường tròn đã cho.
Bài 12 trang 53 SGK Hình học 12 Nâng cao
Trong mỗi trường hợp sau, gọi tên hình tròn xoay: a) Sinh bởi ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư. b) Sinh bởi một hình chữ nhật (kể cả điểm trong) khi quay quanh đường thẳng chứa một cạnh.
Bài 11 trang 53 SGK Hình học 12 Nâng cao
Chứng ming rằng hình tròn xoay có vô số mặt phẳng đối xứng.