Giải bài 9.25 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức

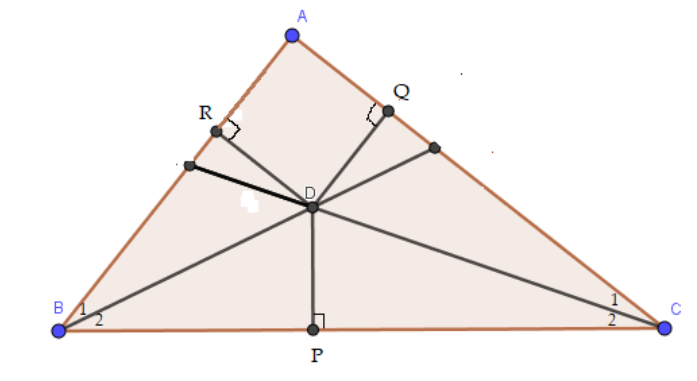
Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB. a) Hãy giải thích tại sao DP = DR. b) Hãy giải thích tại sao DP = DQ. c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)

Toán - Văn - Anh - Khoa học tự nhiên...

Đề bài

Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.

a) Hãy giải thích tại sao DP = DR.

b) Hãy giải thích tại sao DP = DQ.

c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)

Phương pháp giải - Xem chi tiết

Sử dụng tính chất tia phân giác của một góc, xét 2 tam giác bằng nhau, suy ra các cạnh tương ứng bằng nhau.

Lời giải chi tiết

a) Vì BD là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)

Vì CD là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)

Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:

\(\widehat {{B_2}} = \widehat {{B_1}}\)

BD chung

\( \Rightarrow \Delta BDP = \Delta BDR\) ( cạnh huyền – góc nhọn)

\( \Rightarrow \) DP = DR ( 2 cạnh tương ứng) (1)

b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:

\(\widehat {{C_2}} = \widehat {{C_1}}\)

CD chung

\( \Rightarrow \Delta CDP = \Delta CDQ\) ( cạnh huyền – góc nhọn)

\( \Rightarrow \) DP = DQ ( 2 cạnh tương ứng) (2)

c) Từ (1) và (2), ta được: DR = DQ ( cùng bằng DP).

D nằm trên tia phân giác của góc A do D cách đều AB và AC.

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 36 phiếu

Giải bài 9.24 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
Giải bài 9.23 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120
Giải bài 9.22 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Giải bài 9.21 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
Chứng minh rằng: a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau. b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Giải bài 9.20 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức: BG = ? BN, CG = ? CP; BG = ? GN, CG = ? GP.
Giải mục 2 trang 74,75 SGK Toán 7 tập 2 - Kết nối tri thức
Mỗi tam giác có mấy đường phân giác?
Giải mục 1 trang 72 SGK Toán 7 tập 2 - Kết nối tri thức
Mỗi tam giác có mấy đường trung tuyến?