 Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
 Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường ..
Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường ..
Giải bài 9.22 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Tổng hợp đề thi giữa kì 2 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - KHTN...
Đề bài
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Phương pháp giải - Xem chi tiết
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác GBC để so sánh BG và CG.
Sử dụng định lí về sự đồng quy của ba đường trung tuyến trong tam giác để so sánh BM và CN.
Lời giải chi tiết
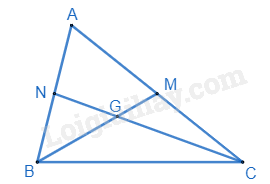
Xét tam giác BGC có \( \widehat {GBC} > \widehat {GCB} \) suy ra CG > BG (1)
Hai đường trung tuyến BM và CN cắt nhau tại G nên theo định lí về sự đồng quy của ba đường trung tuyến trong tam giác ta có:
\( CG = \frac{2}{3}CN; BG = \frac{2}{3}BM\) (2)
Từ (1) và (2) suy ra CN > BM.
- Giải bài 9.23 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
- Giải bài 9.24 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
- Giải bài 9.25 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
- Giải bài 9.21 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
- Giải bài 9.20 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Giải mục 2 trang 104 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2












Danh sách bình luận