Bài 5.17 trang 20 SBT Vật lí 6
Giải bài 5.17 trang 20 sách bài tập vật lí 6. Trong phòng thí nghiệm, người ta còn dùng cân Rô-béc-van để xác định chính xác thể tích của một vật rắn không thấm nước. Cách làm như sau:
Đề bài
Trong phòng thí nghiệm, người ta còn dùng cân Rô-béc-van để xác định chính xác thể tích của một vật rắn không thấm nước. Cách làm như sau:
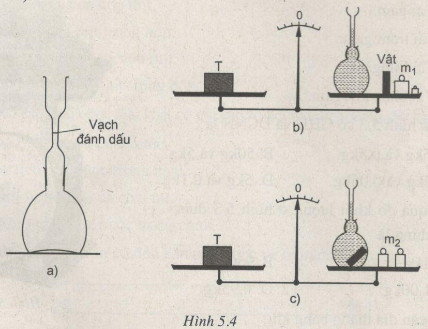
- Dùng một loại bình đặc biệt có nút rỗng bằng thuỷ tinh có thể vặn khít vào cổ bình. Giữa nút có một ống thủy tinh nhỏ, trên có khắc một "vạch đánh dấu" cho phép xác định một cách chính xác thể tích của nước trong bình tới vạch đánh dấu (H.5.4a).
- Dùng cân Rô-béc-van cân hai lần:
+ Lần thứ nhất: Đặt lên đĩa cân bình chứa nước cất tới vạch đánh dấu, vật cần xác định thể tích, các quả cân có khối lượng tổng cộng là\(m_1\), sao cho cân bằng với một vật nặng T đặt trên đĩa cân còn lại (vật T được gọi là tải) (H.5.4b)
+ Lần thứ hai: Lấy bình ra khỏi đĩa cân, mở nút, đổ bớt nước cất trong bình, thả vật cần xác định thể tích vào bình, đậy nút và cho thêm nước vàc bình tới vạch đánh dấu, rồi đặt lại bình lên đĩa cân. Thay các quả cân khối lượng \(m_1\) bằng các quả cân khối lượng \(m_2\) để cân lại cân bằne (H.5.4c)
Biết \(1g\) nước cất có thể tích bằng \(1c{m^3}\). Hãy chứng minh rằng thể tích V của vật tính ra \(c{m^3}\) có độ lớn đúng bằng độ lớn của hiệu các khối lượng \({m_2} - {m_1}\) tính ra \(g\).
Tại sao cách xác định thể tích này lại chính xác hơn cách đo thể tích vật rắn bằng bình chia độ?
Phương pháp giải - Xem chi tiết
Sử dụng lí thuyết về cân Rô-béc-van.
Lời giải chi tiết
Lần cân thứ nhất cho: \({m_T} = {m_b} + {m_n} + {m_v} + {m_1}\)
Lần cân thứ hai cho: \({m_T} = {m_b} + ({m_n} - {m_{{n_0}}}) + {m_v} + {m_2}\)
Trong phương trình (1), \({m_n}\) là khối lượng của nước chứa trong bình tới vạch đánh dấu, \({m_b}\) là khối lượng bình, \({m_v}\) là khối lượng vật.
Trong phương trình (2), \({m_{{n_0}}}\) là khối lượng của phần nước bị vật chiếm chỗ.
Từ (1) và (2), ta có \({m_{{n_0}}}={m_2}-{m_1}\)
- Vì \(1\)gam nước nguyên chất có thể tích là \(1c{m^3}\), nên số đo khối lượng \({m_{{n_0}}}\) theo đơn vị gam là số đo thể tích của phần nước bị vật chiếm chỗ theo đơn vị \(c{m^3}\). Thể tích của phần nước bị vật chiếm chỗ chính là thể tích của vật, do đó thể tích của vật tính ra \(c{m^3}\) có độ lớn bằng \(({m_2}-{m_1})\) .
- Cách xác định vật thể như trên chính xác hơn cách xác định bằng bình chia độ, đo khối lượng bằng cân Rô-béc-van chính xác hơn đo thể tích bằng bình chia độ do:
+) GHĐ của cân Rô-béc-van nhỏ hơn GHĐ của bình chia độ rất nhiều.
+) Cách đọc mực nước ở bình chia độ khó chính xác hơn cách theo dõi kim của cân ở vị trí cân bằng. Mặt khác, cách cân hai lần như trên loại trừ được những sai số đo do cân cấu tạo không được tốt, chẳng hạn hai phần của đòn cân không thật bằng nhau về chiều dài cũng như khối lượng.
Loigiaihay.com













Danh sách bình luận