Ôn tập chương 4 - Kết nối tri thức với cuộc sống

Giải bài 4.56 trang 73 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

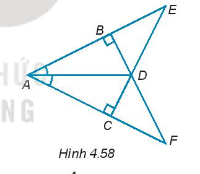
Cho các điểm A, B, C, D, E, F như Hình 4.58. a)Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho các điểm A, B, C, D, E, F như Hình 4.58.

a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

b) Chứng minh \(\Delta ADE = \Delta ADF\).

Phương pháp giải - Xem chi tiết

a) Các cặp tam giác bằng nhau:

- \(\Delta ABD = \Delta ACD\left( {ch - gn} \right)\)

- \(\Delta ABF = \Delta ACE\left( {ch - cgv} \right)\)

- \(\Delta BDE = \Delta CDF\left( {g - c - g} \right)\)

b) \(\Delta ADE = \Delta ADF\left( {c - g - c} \right)\)

Lời giải chi tiết

- Xét \(\Delta ABD\) và \(\Delta ACD\) có:

AD: Cạnh chung

\(\widehat {DAB} = \widehat {DAC} (gt)\)

\(\widehat {ABD} = \widehat {ACD} = {90^0}\)

Vậy \(\Delta ABD = \Delta ACD\left( {ch - gn} \right)\)

- Xét \(\Delta ABF\) và \(\Delta ACE\) có:

\(\begin{array}{l}AB = AC\left( \text{do } \Delta ABD = \Delta ACD \right)\\\widehat A: \text{ chung}\\\widehat {ABF} = \widehat {ACE} = {90^0}\end{array}\)

Vậy \(\Delta ABF = \Delta ACE\left( {ch - cgv} \right)\)

- Xét \(\Delta BDE\) và \(\Delta CDF\) có:

\(\begin{array}{l}\widehat {DBE} = \widehat {DCF} = {90^0}\\BD = CD\left(\text{do } \Delta ABD = \Delta ACD \right)\\\widehat {BDE} = \widehat {CDF}\left( \text{hai góc đối đỉnh} \right)\end{array}\)

Vậy \(\Delta BDE = \Delta CDF\left( {g - c - g} \right)\)

b) Ta có:

\(\Delta ABF = \Delta ACE\left( {cmt} \right) \) nên \(AF = AE\)

\(\Delta BDE = \Delta CDF\left( {cmt} \right) \) nên \(\widehat E = \widehat F\)

Xét \(\Delta ADE\) và \(\Delta ADF\) có:

\(AD\): Cạnh chung

\(AE = AF (cmt)\)

\(\begin{array}{l}\widehat E = \widehat F\left( {cmt} \right) \end{array}\)

Vậy \(\Delta ADE = \Delta ADF\left( {c - g - c} \right)\)

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 16 phiếu

Bài tiếp theo

Giải bài 4.57 trang 73 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59) a)Chứng minh rằng MP = MQ và AP = AQ b) Đường thẳng PQ có vuông góc với AM không? Vì sao?
Giải bài 4.58 trang 74 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB.
Giải bài 4.59 trang 74 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.
Giải bài 4.60 trang 74 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho hình thang cân ABCD có đáy lớn AD đáy nhỏ BC thoả mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD
Giải bài 4.55 trang 73 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho các điểm A, B, C, D như Hình 4.57
Giải bài 4.54 trang 73 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Tính số đo các góc chưa biết của các tam giác dưới đây (h.4.56)
Giải bài 4.53 trang 72 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Trong các câu sau đây, câu nào đúng, câu nào sai? a)Tam giác cân có một góc bằng 60 độ là tam giác đều. b) Tam giác cân là tam giác nhọn. c) Tổng hai góc nhọn của một tam giác vuông bằng 90 độ. d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45 độ.
Giải bài 4.52 trang 72 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Trong các câu sau đây, câu nào đúng, câu nào sai? a) Tam giác nhọn có ba góc đều nhọn. b) Tam giác vuông có đúng hai góc nhọn. c) Tam giác tù có đúng một góc nhọn. d) Trong ba góc của một tam giác tù, góc tù có số đo lớn nhất.
Giải bài 4.51 trang 72 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Tính số đo các góc x, y, z, t, v trong hình 4.55
Giải Câu hỏi trắc nghiệm trang 71, 72 sách bài tập Toán 7 Kết nối tri thức với cuộc sống
Tìm câu trả lời đúng trong các đáp án đã cho