Bài 15: Các trường hợp bằng nhau của tam giác vuông - K..

Giải bài 4.36 trang 65 sách bài tập toán 7 - Kết nối tri thức với cuộc sống


Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng

Đề bài

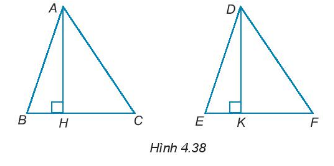
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng \(\Delta ABC = \Delta DEF\). Hãy chứng minh AH = DK.

Phương pháp giải - Xem chi tiết

Chứng minh \(\Delta HAB = \Delta KDE\left( {ch - gn} \right)\)

Lời giải chi tiết

Ta có:

\(\begin{array}{l}\Delta ABC = \Delta DEF\\ \Rightarrow \left\{ \begin{array}{l}AB = DE\\\widehat {ABC} = \widehat {DEF} hay \widehat {HBA} = \widehat {KED}\end{array} \right.\end{array}\)

Xét \(\Delta HAB\) và \(\Delta KDE\) có:

\(\widehat {AHB} = \widehat {DKE} = {90^0}\\AB = DE\\\widehat {HBA} = \widehat {KED}\left( {cmt} \right)\\ \Rightarrow \Delta HAB = \Delta KDE\left( {ch - gn} \right)\)

\(\Rightarrow AH = DK\) (2 cạnh tương ứng)


Bình chọn:
4.4 trên 16 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store