Giải bài 4.16 trang 74 SGK Toán 7 tập 1 - Kết nối tri thức

Cho hai tam giác ABC và DEF thoả mãn

Đề bài

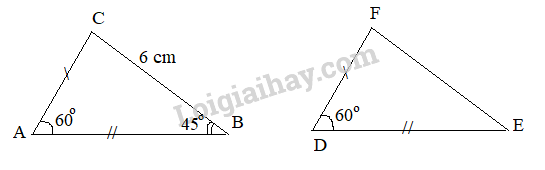
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Phương pháp giải - Xem chi tiết

Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh

Từ đó suy ra các cặp cạnh và các cặp góc tương ứng bằng nhau

Lời giải chi tiết

Xét hai tam giác ABC và DEF có:

\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)

\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)

Do đó:

\(BC=EF = 6cm\) ( 2 cạnh tương ứng)

\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)

\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)

\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)