-
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
-
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Giải bài 2 trang 74 sách bài tập toán 10 - Chân trời sáng tạo
a) Tính các góc, các cạnh còn lại của tam giác ABC b) Tính bán kính đường tròn ngoại tiếp của tam giác ABC
Đề bài
Cho tam giác ABC , biết cạnh \(a = 75\) cm, \(\widehat B = 80^\circ ,\widehat C = 40^\circ \)
a) Tính các góc, các cạnh còn lại của tam giác ABC
b) Tính bán kính đường tròn ngoại tiếp của tam giác ABC
Lời giải chi tiết
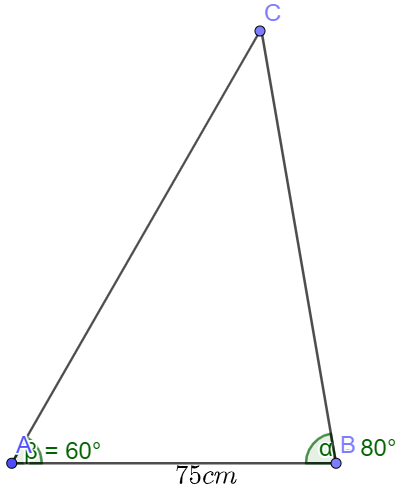
a) Ta có \(\widehat A + \widehat B + \widehat C = 180^\circ \)
Suy ra \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) = 180^\circ - \left( {80^\circ + 40^\circ } \right) = 60^\circ \)
Áp dụng định lí sin ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Leftrightarrow \frac{{AB}}{{\sin 40^\circ }} = \frac{{75}}{{\sin 60^\circ }} = \frac{{AC}}{{\sin 80^\circ }} = 50\sqrt 3 \end{array}\)
\( \Rightarrow AB \simeq 55,67;AC \simeq 85,29\)
b) Ta có \(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{{75}}{{2.\sin 60^\circ }} = 25\sqrt 3 \)
Bình luận
Chia sẻ
- Giải bài 3 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 4 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 5 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 6 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
- Giải bài 7 trang 75 sách bài tập toán 10 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
