-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài tập ôn tập chương II
Câu 7 trang 78 SGK Hình học 11 Nâng cao
Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho \({{AM} \over {AB}} = {{D'N} \over {D'D}} = {{B'P} \over {B'C'}}\)
a. Chứng minh rằng mp(MNP) và mp(AB'D’) song song với nhau
b. Xác định thiết diện của hình hộp khi cắt bởi mp(MNP)
Quảng cáo
Lời giải chi tiết
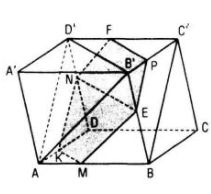
a. Kẻ ME song song với AB’ (E ∈ BB’) (1)
Ta có: \(\eqalign{ & {{B'E} \over {B'B}} = {{AM} \over {AB}} \Rightarrow {{B'E} \over {B'B}} = {{B'P} \over {B'C'}} \cr & \cr} \)
⇒ EP // BC’ ⇒EP // AD’ (2)
Từ (1) và (2) suy ra (MEP) // (AB’D’) (3)
Rõ ràng D’N = B’E nên EN // B’D’
Mà B’D’ ⊂ (AB’D’) và E ∈ (MEP) nên từ (3) suy ra EN ⊂ (MEP), tức (MNP) chính là (MEP)
Vậy (MNP) // (AB’D’)
b. Từ M kẻ ME song song với AB’, từ P kẻ PF song song với B’D’. Từ N kẻ NK song song với AD’ cắt AD tại K
Thiết diện là lục giác MEPFNK có các cạnh đối song song
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 8 trang 78 SGK Hình học 11 Nâng cao
- Câu 6 trang 78 SGK Hình học 11 Nâng cao
- Câu 5 trang 78 SGK Hình học 11 Nâng cao
- Câu 4 trang 78 SGK Hình học 11 Nâng cao
- Câu 3 trang 77 SGK Hình học 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
