Câu 4 trang 120 SGK Hình học 11 Nâng cao

Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng

Đề bài

Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng \({\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \)

Phương pháp giải - Xem chi tiết

Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

Lời giải chi tiết

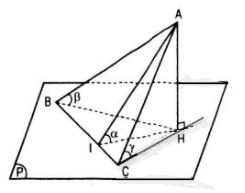
Kẻ AH ⊥ mp(P) và AI ⊥ BC.

Khi đó HB là hình chiếu của AB trên (P) nên góc giữa AB và (P) bằng góc giữa AB và HB hay \(\beta = \widehat {ABH}\)

HC là hình chiếu của AC trên (P) nên góc giữa AC và (P) bằng góc giữa AC và HC hay \(\gamma = \widehat {ACH}\)

Lại có:

\(\left\{ \begin{array}{l}
AI \bot BC\\
AH \bot BC\left( {AH \bot \left( P \right)} \right)
\end{array} \right. \) \(\Rightarrow BC \bot \left( {AIH} \right) \Rightarrow BC \bot HI\)

Mà \(BC \bot AI\) và \(\left( {ABC} \right) \cap \left( P \right) = BC\) nên góc giữa (ABC) và (P) bằng góc giữa AI và HI hay \(\alpha = \widehat {AIH}.\) (do \(\widehat {AIH}<90^0\)).

Vì ΔABC vuông ở A nên :

\(\eqalign{ & {1 \over {A{I^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} \cr & \Rightarrow {{A{H^2}} \over {A{I^2}}} = {{A{H^2}} \over {A{B^2}}} + {{A{H^2}} \over {A{C^2}}} \cr & hay\,\,{\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \cr} \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Câu 5 trang 120 SGK Hình học 11 Nâng cao
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Câu 6 trang 120 SGK Hình học 11 Nâng cao
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABB’A’ là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB’.
Câu 7 trang 121 SGK Hình học 11 Nâng cao
Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :
Câu 8 trang 121 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
Câu 3 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
Câu 2 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABC có SA = Sb = SC = a,
Câu 1 trang 120 SGK Hình học 11 Nâng cao
Tứ diện OABC có OA = OB = OC = a và