Câu 2 trang 120 SGK Hình học 11 Nâng cao

Cho hình chóp S.ABC có SA = Sb = SC = a,

Đề bài

Cho hình chóp S.ABC có SA = SB = SC = a, \(\widehat {ASB} = 120^\circ ,\widehat {BSC} = 60^\circ ,\widehat {CSA} = 90^\circ \) .

a. Chứng tỏ rằng ABC là tam giác vuông

b. Tính khoảng cách từ S đến mặt phẳng (ABC)

Quảng cáo

Lời giải chi tiết

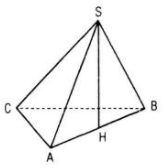
a. Ta có:

\(\eqalign{ & \overrightarrow {CA} .\overrightarrow {CB} \cr &= \left( {\overrightarrow {SA} - \overrightarrow {SC} } \right)\left( {\overrightarrow {SB} - \overrightarrow {SC} } \right) \cr & = \overrightarrow {SA} .\overrightarrow {SB} - \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SC} .\overrightarrow {SB} + S{C^2} \cr & = {a^2}\cos 120^\circ - {a^2}\cos 90^\circ - {a^2}\cos 60^\circ + {a^2} \cr & = {a^2} - {{{a^2}} \over 2} - {{{a^2}} \over 2} = 0 \cr & \Rightarrow CA \bot CB \cr} \)

⇒ ΔABC vuông tại C.

b. Kẻ SH ⊥ mp(ABC), do SA = SB = SC nên HA = HB = HC mà ΔABC vuông tại C nên H là trung điểm của AB.

Áp dụng định lí cô sin vào tam giác ABC, ta có:

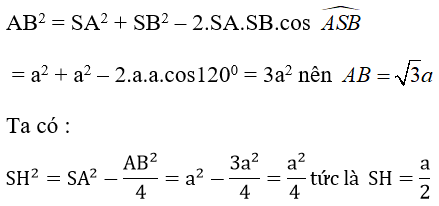
Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 6 phiếu

Bài tiếp theo

Câu 3 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
Câu 4 trang 120 SGK Hình học 11 Nâng cao
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng
Câu 5 trang 120 SGK Hình học 11 Nâng cao
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Câu 6 trang 120 SGK Hình học 11 Nâng cao
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABB’A’ là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB’.
Câu 7 trang 121 SGK Hình học 11 Nâng cao
Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :
Câu 8 trang 121 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
Câu 1 trang 120 SGK Hình học 11 Nâng cao
Tứ diện OABC có OA = OB = OC = a và