Bài tập cuối tuần Toán 5 tuần 35 - Đề 1 (Có đáp án và lời giải chi tiết)
Tải vềBài tập cuối tuần 35 - Đề 1 bao gồm các bài tập chọn lọc với dạng bài tập giúp các em ôn tập lại kiến thức đã được học trong tuần
Đề bài
Bài 1. Đúng ghi Đ, sai ghi S:
Số thập phân 620,06 thay đổi thế nào khi:
a) Chuyển dấu phẩy sang phải một chữ số?
Gấp lên 10 lần …..
Giảm đi 10 lần …..
Tăng lên 5580,54 đơn vị …..
Giảm đi 5580,54 đơn vị …..
b) Chuyển dấu phẩy sang trái hai chữ số?
Gấp lên 100 lần …..
Giảm đi 100 lần …..
Tăng lên 613,8594 đơn vị …..
Giảm đi 613,8594 đơn vị …..
Bài 2. Tính:
a) \(\dfrac{2}{5} \times \dfrac{3}{4} + \dfrac{2}{5}:\dfrac{4}{9} \times 5\)
b) \(\dfrac{{25}}{{12}} \times \dfrac{{18}}{{35}} \times \dfrac{{63}}{{24}}\)
c) (25,46 – 56,42 : 4) + 16,5 × 23;
d) (32,5 + 28,3 × 2,7 – 108,91) × 2006.
Bài 3. Biểu đồ dưới đây thống kê các loại sách trong thư viện của một trường tiểu học:
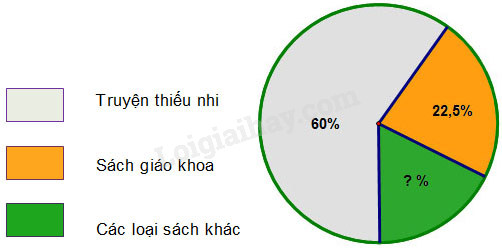
- Em hãy cho biết, biểu đồ thống kế những loại sách nào ?
- Tỉ số phần trăm truyện thiếu nhi là bao nhiêu ? Tỉ số phần trăm sách giáo khoa là bao nhiêu ?
- Trong thư viện có bao nhiêu phần trăm các loại sách khác ?
- Cho biết trong thư viện có tất cả 2000 quyển sách. Hãy tính số sách giáo khoa trong thư viện.
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 4. Một người bán được 72kg gạo nếp và gạo tẻ, trong đó \(\dfrac{1}{2}\) số gạo nếp bằng \(\dfrac{2}{5}\) số gạo tẻ. Hỏi người đó bán được mỗi loại bao nhiêu ki-lô-gam gạo?
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 5. Một người đi xe đạp từ A đến B hết 2 giờ 15 phút với vận tốc 12km/giờ. Lúc B trở về A người đó đi ô tô hết 25 phút. Tính vận tốc của ô tô.
Bài giải
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Lời giải chi tiết
Bài 1.
Phương pháp:
- Dựa vào cách nhân một số thập phân với 10, 100, 1000; …
- Tìm số thập phân thu được sau khi dịch chuyển dấu phẩy rồi tìm hiệu của số mới và số ban đầu.
Cách giải:
a) Khi chuyển dấu phẩy của số thập phân 620,06 sang phải một chữ số ta được số 6200,6.
Số 6200,6 gấp 10 lần số 620,06 hay số mới gấp 10 lần số ban đầu.
Số 6200,6 hơn số 620,06 số đơn vị là:
6200,6 – 620,06 = 5580,64
Vậy ta có kết quả như sau:
Gấp lên 10 lần (Đ)
Giảm đi 10 lần (S)
Tăng lên 5580,54 đơn vị (Đ)
Giảm đi 5580,54 đơn vị (S)
b) Khi chuyển dấu phẩy của số thập phân 620,06 sang trái hai chữ số ta được số 6,2006.
Số 620,06 gấp 100 lần số 6,2006 hay số mới giảm 100 lần so với số ban đầu.
Số 620, 06 hơn số 6,2006 số đơn vị là:
620,06 – 6,2006 = 613,85994
Vậy ta có kết quả như sau:
Gấp lên 100 lần (S)
Giảm đi 100 lần (Đ)
Tăng lên 613,8594 đơn vị (S)
Giảm đi 613,8594 đơn vị (Đ)
Bài 2:
Phương pháp:
- Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
- Biểu thức chỉ có phép tính cộng, trừ hoặc chỉ có phép tính nhân, chia thì thực hiện theo thứ tự từ trái sang phải.
- Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Cách giải:
a) \(\dfrac{2}{5} \times \dfrac{3}{4} + \dfrac{2}{5}:\dfrac{4}{9} \times 5\)\( = \dfrac{2}{5} \times \dfrac{3}{4} + \dfrac{2}{5} \times \dfrac{9}{4} \times 5\)
\( = \dfrac{2}{5} \times \left( {\dfrac{3}{4} + \dfrac{9}{4} \times 5} \right)\)\( = \dfrac{2}{5} \times \left( {\dfrac{3}{4} + \dfrac{{45}}{4}} \right)\)
\( = \dfrac{2}{5} \times \dfrac{{48}}{4} = \dfrac{2}{5} \times 12 = \dfrac{{24}}{5}\)
b) \(\dfrac{{25}}{{12}} \times \dfrac{{18}}{{35}} \times \dfrac{{63}}{{24}}\)\( = \dfrac{{25 \times 18 \times 63}}{{12 \times 35 \times 24}}\)\( = \dfrac{{5 \times 5 \times 6 \times 3 \times 3 \times 21}}{{6 \times 2 \times 7 \times 5 \times 3 \times 8}}\)
\( = \dfrac{{5 \times 3 \times 21}}{{2 \times 7 \times 8}} = \dfrac{{5 \times 3 \times 2 \times 7}}{{2 \times 7 \times 8}}\)\( = \dfrac{{15}}{8}\)
c) (25,46 – 56,42 : 4) + 16,5 × 23
= (25,46 – 14,105) + 379,5
= 11,355 + 379,5
= 390,855
d) (32,5 + 28,3 × 2,7 – 108,91) × 2006
= (32,5 + 76,41 – 108, 91) × 2006
= (108,91 – 108,91) × 2006
= 0 × 2006
= 0
Bài 3.
Phương pháp:
- Quan sát biểu đồ để tìm các loại sách được thống kê và tỉ số phần trăm của các loại sách đó.
- Muốn tìm số sách giáo khoa ta có thể lấy tổng số sách trong thư viện chia cho 100 rồi nhân với 22,5 hoặc lấy tổng số sách trong thư viện nhân với 22,5 rồi chia cho 100 (vì tỉ số phần trăm sách giáo khoa là 22,5%.)
Cách giải:
- Biểu đồ thống kế các loại sách là : Truyện thiếu nhi, sách giáo khoa và các loại sách khác.
- Tỉ số phần trăm truyện thiếu nhi là 60%.
Tỉ số phần trăm sách giáo khoa là 22,5%.
- Số phần trăm các loại sách khác trong thư viện là :
100 – (60 + 22,5) = 17,5%
- Số sách giáo khoa trong thư viện là :
2000 : 100 × 22,5 = 450 (quyển sách)
Bài 4:
Phương pháp:
Viết: \(\dfrac{1}{2} = \dfrac{2}{4}\). Khi đó ta có \(\dfrac{2}{4}\) số gạo nếp bằng \(\dfrac{2}{5}\) số gạo tẻ. Do đó nếu coi số gạo nếp gồm 4 phần bằng nhau thì số gạo tẻ gồm 5 phần như thế.
Tìm số gạo mỗi loại theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Cách giải:
Ta có: \(\dfrac{1}{2} = \dfrac{2}{4}\).
Khi đó ta có \(\dfrac{2}{4}\) số gạo nếp bằng \(\dfrac{2}{5}\) số gạo tẻ. Do đó nếu coi số gạo nếp gồm 4 phần bằng nhau thì số gạo tẻ gồm 5 phần như thế.
Ta có sơ đồ:
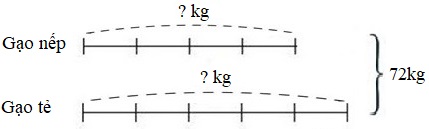
Theo sơ đồ, tổng số phần bằng nhau là:
4 + 5 = 9 (phần)
Người đó bán được số ki-lô-gam gạo nếp là:
72 : 9 × 4 = 32 (kg)
Người đó bán được số ki-lô-gam gạo tẻ là:
72 – 32 = 40 (kg)
Đáp số: Gạo nếp: 32kg
Gạo tẻ: 40kg.
Bài 5.
Phương pháp:
- Đổi các số đo thời gian về số đo có đơn vị ta giờ.
- Tìm độ dài quãng đường AB ta lấy vận tốc đi xe đạp nhân với thời gian người đi xe đạp đi hết quãng đường AB.
- Tìm vận tốc của ô tô ta lấy độ dài quãng đường AB chia cho thời gian người đi xe đạp đi hết quãng đường AB.
Cách giải:
Đổi: 2 giờ 15 phút = 2,25 giờ; 25 phút = \(\dfrac{5}{{12}}\) giờ
Quãng đường từ A đến B dài số ki-lô-mét là:
12 × 2,25 = 27 (km)
Vận tốc của ô tô là:
27 : \(\dfrac{5}{{12}}\) = 64,8 (km/giờ)
Đáp số: 64,8 km/giờ.
Loigiaihay.com
Các bài khác cùng chuyên mục
- Bài tập cuối tuần Toán 5 tuần 7 - Đề 2 ( Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 33 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 33 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 35 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 35 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 33 - Đề 2 (Có đáp án và lời giải chi tiết)













Danh sách bình luận