Bài tập cuối tuần Toán 5 có đáp án và lời giải chi tiết

Bài tập cuối tuần 2

Bài tập cuối tuần Toán 5 tuần 2 - Đề 1 (Có đáp án và lời giải chi tiết)

Tải về

Bài tập cuối tuần 2 - Đề 2 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần

Đề bài

Bài 1: Đúng ghi Đ, sai ghi S:

a) \(4 + \dfrac{2}{{25}} = \dfrac{{102}}{{25}}\)	b) \(5 - \dfrac{4}{{13}} = \dfrac{1}{{13}}\)
c) \(11 - \dfrac{5}{6} = \dfrac{6}{6}\)	d) \(7 + \dfrac{8}{9} = \dfrac{{71}}{9}\)

Bài 2: Đúng ghi Đ, sai ghi S:

a) \(12 \times \dfrac{1}{3} = \dfrac{1}{{36}}\)	b) \(12 \times \dfrac{1}{3} = \dfrac{{12}}{3}\)
c) \(35:\dfrac{7}{6} = \dfrac{{245}}{6}\)	d) \(35:\dfrac{7}{6} = \dfrac{6}{5}\)
e) \(\dfrac{{49}}{{12}}:7 = \dfrac{7}{{12}}\)	f) \(\dfrac{{49}}{{12}}:7 = \dfrac{{49}}{{84}}\)

Bài 3: Khoanh vào chữ cái đặt trước câu trả lời đúng:

Tính: \(4-\dfrac{3}{5}+\dfrac{2}{5}\)

A. \(3\)

B. \(\dfrac{3}{10}\)

C. \(\dfrac{19}{5}\)

Bài 4: Khoanh vào chữ đặt trước câu trả lời đúng:

Một miếng bìa hình chữ nhật có diện tích \(\dfrac{22}{5}m^2\), chiều dài là \(\dfrac{5}{6}m\). Tính chiều rộng của miếng bìa đó.

A. \(\dfrac{11}{3}m\)

B. \(\dfrac{132}{25}m\)

C. \(\dfrac{25}{132}m\)

Bài 5: Tính:

a) \(\dfrac{1}{5}-\dfrac{1}{5}\times\dfrac{1}{5}\)

…………………

b) \(\dfrac{7}{18}+\dfrac{6}{5}:\dfrac{5}{2}\)

…………………

c) \(\dfrac{9}{12}\times\dfrac{8}{7}:\dfrac{3}{22}\)

…………………

d) \(\dfrac{25}{23}:\dfrac{16}{9}\times \dfrac{46}{75}\)

…………………...

……………………

Bài 6: Tìm x biết:

a) \(x+\dfrac{5}{21}\)\(=\dfrac{1}{6}+\dfrac{1}{3}\)

…………………

b) \(x-\dfrac{19}{32}\)\(=\dfrac{5}{6}-\dfrac{2}{3}\)

………………

c) \(x\times \dfrac{4}{3}\)\(=\dfrac{9}{16}:\dfrac{15}{32}\)

……………………

d) \(x:\dfrac{28}{5}\)\(=\dfrac{14}{23}\times\dfrac{23}{12}\)

……………………

Bài 7: Một bồn hoa hình chữ nhật có chiều dài là \(\dfrac{17}{4}m\), chiều rộng kém chiều dài \(\dfrac{1}{3}m.\) Tính chu vi và diện tích của bồn hoa đó.

........................................................................................................................................

Lời giải chi tiết

Bài 1:

Phương pháp giải:

Để cộng hoặc trừ số tự nhiên và phân số ta viết số tự nhiên dưới dạng phân số rồi quy đồng mẫu số các phân số, sau đó cộng các tử số hoặc trừ các tử số và giữ nguyên mẫu số.

Cách giải:

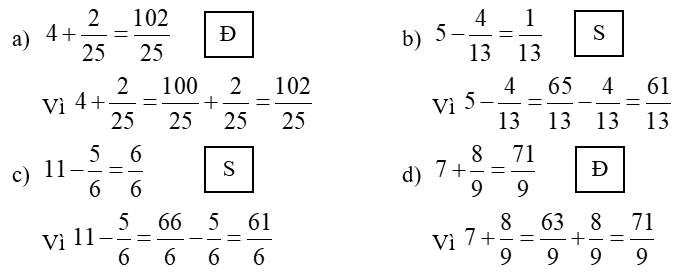
Bài 2:
Phương pháp giải:

- Khi nhân một số với một phân số thì ta nhân số đó với tử số và giữ nguyên mẫu số.

- Khi chia một số (hoặc 1 phân số) cho 1 phân số thì ta lấy số đó (hoặc phân số đó) nhân với phân số nghịch đảo của số chia. Trường hợp số chia là số tự nhiên thì ta coi số đó là phân số có mẫu số là 1.

Cách giải:

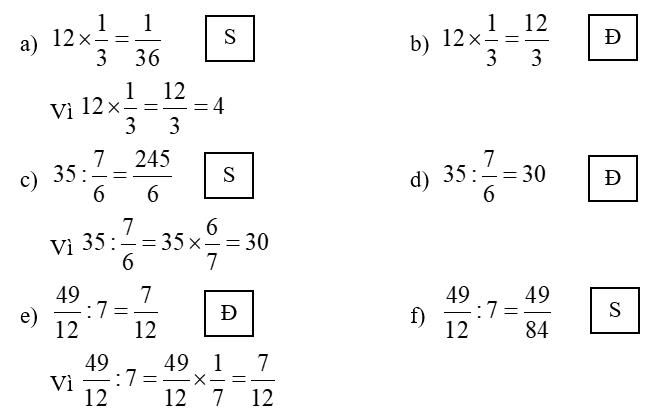
Bài 3:

Phương pháp giải:

Biểu thức chỉ có phép cộng và phép trừ thì thực hiện tính theo thứ tự từ trái sang phải.

Cách giải:

\(4 - \dfrac{3}{5} + \dfrac{2}{5} = \dfrac{{20}}{5} - \dfrac{3}{5} + \dfrac{2}{5}\)\( = \dfrac{{17}}{5} + \dfrac{2}{5} = \dfrac{{19}}{5}\)

Vậy đáp án đúng là C.

Bài 4:

Phương pháp giải:

Ta có : Diện tích hình chữ nhật = chiều dài × chiều rộng.

Do đó: chiều rộng = diện tích : chiều dài.

Cách giải:

Chiều rộng của miếng bìa hình chữ nhật là:

\(\dfrac{{22}}{5}:\dfrac{5}{6} = \dfrac{{22}}{5} \times \dfrac{6}{5} = \dfrac{{132}}{{25}}\,\,(m)\)

Đáp án: \(\dfrac{{132}}{{25}}m\).

Vậy đáp án đúng là B.

Bài 5:

Phương pháp giải:

- Biểu thức chỉ có phép nhân và phép chia thì thực hiện tính theo thứ tự từ trái sang phải.

- Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép tính nhân, chia trước; thực hiện phép cộng, trừ sau.

Cách giải:

a) \(\dfrac{1}{5} - \dfrac{1}{5} \times \dfrac{1}{5}\)

\( = \dfrac{1}{5} - \dfrac{1}{{25}}\)

\( = \dfrac{5}{{25}} - \dfrac{1}{{25}}\)

\( = \dfrac{4}{{25}}\)

b) \(\dfrac{7}{{18}} + \dfrac{6}{5}:\dfrac{5}{2}\)

\( = \dfrac{7}{{18}} + \dfrac{6}{5} \times \dfrac{2}{5}\)

\( = \dfrac{7}{{18}} + \dfrac{{12}}{{25}}\)

\( = \dfrac{{175}}{{450}} + \dfrac{{216}}{{450}}\)

\( = \dfrac{{391}}{{450}}\)

c) \(\dfrac{9}{{12}} \times \dfrac{8}{7}:\dfrac{3}{{22}}\)

\( = \dfrac{6}{7}:\dfrac{3}{{22}}\)

\( = \dfrac{6}{7} \times \dfrac{{22}}{3}\)

\(\begin{array}{l} = \dfrac{{6 \times 22}}{{7 \times 3}}\\ = \dfrac{{3 \times 2 \times 22}}{{7 \times 3}}\\ = \dfrac{{44}}{7}\end{array}\)

d) \(\dfrac{{25}}{{23}}:\dfrac{{16}}{9} \times \dfrac{{46}}{{75}}\)

\( = \dfrac{{25}}{{23}} \times \dfrac{9}{{16}} \times \dfrac{{46}}{{75}}\)

\( = \dfrac{{25 \times 9 \times 46}}{{23 \times 16 \times 75}}\)

\( = \dfrac{{25 \times 9 \times 23 \times 2}}{{23 \times 16 \times 25 \times 3}}\)

\(\begin{array}{l} = \dfrac{{9 \times 2}}{{16 \times 3}}\\ = \dfrac{{18}}{{48}} = \dfrac{3}{8}\end{array}\)

Bài 6:

Phương pháp giải:

- Tính giá trị vế phải trước.

- Tìm \(x\) bằng cách áp dụng các quy tắc:

+ Muốn tìm số hạng ta lấy tổng trừ đi số hạng đã biết.

+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.

+ Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

+ Muốn tìm số bị chia ta lấy thương nhân với số chia.

Cách giải:

a) \(x + \dfrac{5}{{21}} \)\(= \dfrac{1}{6} + \dfrac{1}{3}\)

\(x + \dfrac{5}{{21}} = \dfrac{1}{2}\)

\(x = \dfrac{1}{2} - \dfrac{5}{{21}}\)

\(x = \dfrac{{11}}{{42}}\)

b) \(x - \dfrac{{19}}{{32}} \)\(= \dfrac{5}{6} - \dfrac{2}{3}\)

\(x - \dfrac{{19}}{{32}} = \dfrac{1}{6}\)

\(x = \dfrac{1}{6} + \dfrac{{19}}{{32}}\)

\(x = \dfrac{{73}}{{96}}\)

c) \(x \times \dfrac{4}{3} \)\(= \dfrac{9}{{16}}:\dfrac{{15}}{{32}}\)

\(x \times \dfrac{4}{3} = \dfrac{9}{{16}} \times \dfrac{{32}}{{15}}\)

\(x \times \dfrac{4}{3} = \dfrac{6}{5}\)

\(x = \dfrac{6}{5}:\dfrac{4}{3}\)

\(x = \dfrac{9}{{10}}\)

d) \(x:\dfrac{{28}}{5} \)\(= \dfrac{{14}}{{23}} \times \dfrac{{23}}{{12}}\)

\(x:\dfrac{{28}}{5} = \dfrac{7}{6}\)

\(x = \dfrac{7}{6} \times \dfrac{{28}}{5}\)

\(x = \dfrac{{98}}{{15}}\)

Bài 7:

Phương pháp giải:

- Tính chiều rộng của bồn hoa = chiều dài – \(\dfrac{1}{3}\).

- Chu vi của bồn hoa = (chiều dài + chiều rộng) × 2.

- Diện tích của bồn hoa = chiều dài × chiều rộng.

Cách giải:

Chiều rộng của bồn hoa là:

\(\dfrac{{17}}{4} - \dfrac{1}{3} = \dfrac{{47}}{{12}}\) (m)

Chu vi của bồn hoa là:

\((\dfrac{{17}}{4} + \dfrac{{47}}{{12}}) \times 2 = \dfrac{{49}}{3}\) (m)

Diện tích của bồn hoa là:

\(\dfrac{{17}}{4} \times \dfrac{{47}}{{12}} = \dfrac{{799}}{{48}}\) (m²)

Đáp số: Chu vi: \(\dfrac{{49}}{3}\)m;

Diện tích: \(\dfrac{{799}}{{48}}\)cm².

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 13 phiếu

Tải về

Bài tiếp theo

Bài tập cuối tuần Toán 5 tuần 2 - Đề 2 (Có đáp án và lời giải chi tiết)
Bài tập cuối tuần 2 - Đề 2 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần

Luyện Bài Tập Trắc nghiệm Toán lớp 5 - Xem ngay

Báo lỗi - Góp ý