Bài tập cuối tuần Toán 5 tuần 15 - Đề 1 ( Có đáp án và lời giải chi tiết)

Đề bài

PHIẾU BÀI TẬP TOÁN 5 – TUẦN 15

Chủ đề: Chia một số tự nhiên cho một số thập phân – Chia một số thập phân cho một số thập phân.

ĐỀ 1:

Bài 1: Đúng ghi Đ, sai ghi S vào ô trống:

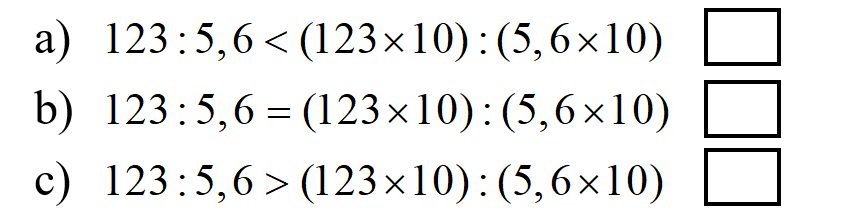
Bài 2: Đúng ghi Đ, sai ghi S vào ô trống:

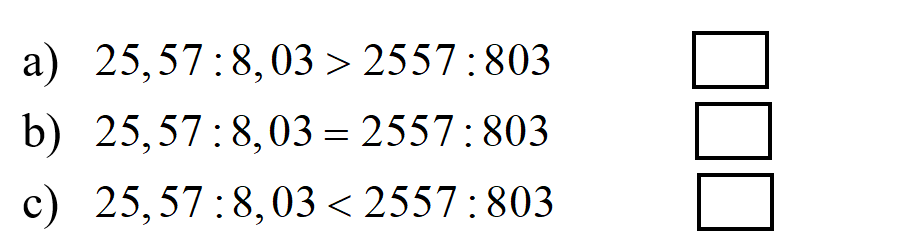
Bài 3: Khoanh vào chữ cái đặt trước câu trả lời đúng:

A. 324 : 5,12 = 63,28 (dư 6,4)                  B. 324 : 5,12 = 63,28( dư 0,64)

C. 324 : 5,12 = 63,28( dư 0,064)              D. 324 : 5,12 = 63,28 ( dư 0,0064)

Bài 4: Tính:

a) \(48,89:2,5+9,01:2,5\)

     ………………………......

     ………………………......

     ………………………......

     ………………………......

     ………………………......

     ………………………......

Bài 5: Tìm \(x\):

a)     \(x \times 1,23 + x \times 5,27 = 227,5\)

        …………………………..................

        …………………………..................

        …………………………..................

        …………………………..................

Bài 6: 

Một khu đất hình thoi có diện tích là 225m², có đường chéo thứ nhất bằng 12,5m.

a) Tính độ dài đường chéo thứ hai của khu đất đó.

b) Cạnh của khu đất bằng \(\dfrac{5}{9}\) độ dài đường chéo thứ hai. Xung quanh khu đất trồng cây, cây nọ cách cây kia 2,5m. Hỏi phải trồng tất cả bao nhiêu cây? 

........................................................................................................................................

........................................................................................................................................

........................................................................................................................................

........................................................................................................................................

........................................................................................................................................

Lời giải chi tiết

Bài 1:

Phương pháp giải:

Áp dụng tính chất: Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đối.

Cách giải:      

Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đối.

Do đó ta có: \(123:5,6 = (123 \times 10):(5,6 \times 10)\).

Vậy ta có kết quả như sau:  

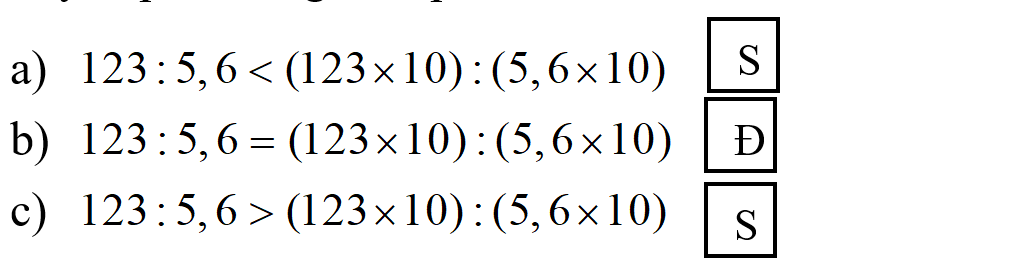
Cách khác: Ta có thể thực hiện phép tính ở hai vế của dấu bằng rồi so sánh kết quả với nhau. Tuy nhiên cách này sẽ dài hơn cách giải bên trên.

Bài 2:

Phương pháp giải:

Áp dụng tính chất: Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đối.

Cách giải:

Khi nhân số bị chia và số chia với cùng một số khác 0 thì thương không thay đối.

Do đó ta có:

 \(25,57:8,03 \)\(= (25,75 \times 100):(8,03 \times 100)\)\( = 2557:803\)

Vậy ta có kết quả như sau:

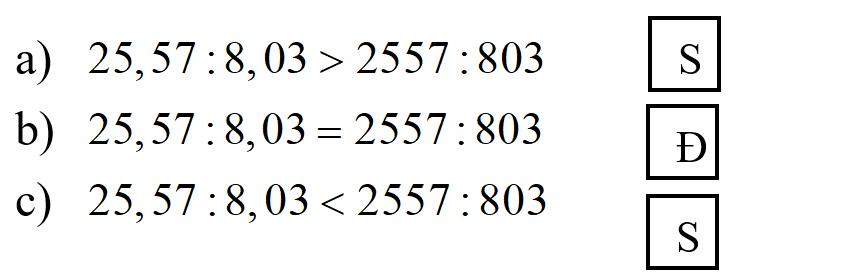
Cách khác: Ta có thể thực hiện phép tính ở hai vế của dấu bằng rồi so sánh kết quả với nhau. Tuy nhiên cách này sẽ dài hơn cách giải bên trên. 

Bài 3:

Phương pháp giải: Ta thực hiện phép chia có dư \(324:5,12\) lấy kết quả thương có hai chữ số ở phần thập phân rồi tìm số dư.

Kiểm tra lại theo công thức:    Số bị chia = thương  × số chia + số dư.

Cách giải:

Đặt tính rồi tính ta có: 

Trong phép chia trên, thương là 63,28 và số dư là 0,0028.

Thử lại: 63,28 ×  5,12 + 0,0064 = 324.

Vậy:   324 : 5,15 = 63,28 (dư 0,0064).

Đáp án đúng là D.

Bài 4:

Phương pháp giải:

Áp dụng các công thức : \(a:c + b:c = (a + b):c\) ;     \(a:c - b:c = (a - b):c\) 

Cách giải: 

a)     \(45,89:2,5 + 9,01:2,5\)

        \(\begin{array}{l} = (45,89 + 9,01):2,5\\ = 54,9:2,5\\ = 21,96\end{array}\)

b)    \(104,32:0,8 - 5,6:0,8\)

        \(\begin{array}{l} = (104,32 - 5,6):0,8\\ = 98,72:0,8\\ = 123,4\end{array}\)

Lưu ý: có thể tính giá trị các biểu thức trên theo quy tắc: biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước, thực hiện phép cộng, trừ sau. Tuy nhiên cách này sẽ dài hơn cách giải bên trên.

Bài 5:

Phương pháp giải:

Đưa về bài toán tìm \(x\) dạng đơn giản hơn bằng cách áp dụng các công thức:

\(a \times b + a \times c = a \times (b + c)\) ;     \(a:c - b:c = (a - b):c\)

Cách giải:

a)     \(x \times 1,23 + x \times 5,27 = 227,5\)

        \(\begin{array}{l}x \times (1,23 + 5,27) = 227,5\\x \times 6,5 = 227,5\\x = 227,5:6,5\\x = 35\end{array}\)

b)    \(36,8:x - 14,2:x = 14,125\)

        \(\begin{array}{l}(36,8 - 14,2):x = 14,125\\22,6:x = 14,125\\x = 22,6:14,125\\x = 1,6\end{array}\)

Bài 6:

Phương pháp giải: Để giải bài toán này cần thực hiện các bước sau:

- Độ dài đường chéo thứ hai = diện tích hình thoi × 2 : độ dài đường chéo thứ nhất.

- Cạnh của khu đất hình thoi = đường chéo thứ hai × \(\dfrac{5}{9}\).

- Chu vi hình thoi = độ dài cạnh hình thoi × 4.

- Số cây phải trồng = chu vi của hình thoi : khoảng cách giữa hai cây liên tiếp.

Cách giải:

a) Độ dài đường chéo thứ hai của khu đất hình thoi là:

                  225× 2 : 12,5 = 36 (m)

b) Độ dài cạnh của khu đất hình thoi là:

                  36 × \(\dfrac{5}{9}\) = 20 (m)

Chu vi của khu đất hình thoi là:

                 20 × 4 = 80 (m)

Số cây phải trồng là:

                 80 : 2,5 = 32 (cây)

                                  Đáp số: a) 36m;

                                               b) 32 cây.