Bài tập cuối tuần Toán 5 tuần 1 - Đề 1 (Có đáp án và lời giải chi tiết)
Tải vềBài tập cuối tuần 1 - Đề 1 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần
Đề bài
Bài 1: Khoanh vào chữ cái đặt trước câu trả lời đúng:
Phân số nào sau đây có tử số bé hơn mẫu số:
| A. \(\dfrac{23}{23}\) | B. \(\dfrac{53}{21}\) | C. \(\dfrac{4}{5}\) | D. \(\dfrac{49}{25}\) |
Bài 2: Điền số thích hợp vào ô trống:
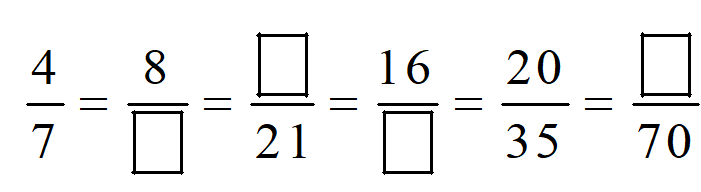
Bài 3: Đúng ghi Đ, sai ghi S vào ô trống:
|
a) \(\dfrac{21}{75}<\dfrac{22}{75}\) |
b) \(\dfrac{21}{75}>\dfrac{22}{75}\) |
|
c) \(\dfrac{37}{26}<\dfrac{37}{27}\) |
|
Bài 4: Khoanh vào chữ đặt trước câu trả lời đúng:
A. Phân số có mẫu số là các số tự nhiên gọi là phân số thập phân.
B. Phân số có mẫu số là 10, 100, 1000, ... gọi là phân số thập phân.
C. Phân số có tử số là 10, 100, 1000, ... gọi là phân số thập phân.
Bài 5: Một hộp bút có 35 cái, trong đó có 12 bút xanh, 10 bút đỏ, còn lại là bút đen. Tìm phân số chỉ số bút xanh so với bút đen, phân số chỉ số bút đỏ so với bút đen.
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 6: Viết rõ phân số rồi rút gọn phân số đó:
a) 45cm = ……………… m = ……………… m.
b) 225m = ……………… km = ……………… km.
c) 15 phút = ……………… giờ = ……………… giờ.
Bài 7: Quãng đường bạn An đi từ nhà đến nhà bà ngoại hết 25km. Trên đường đi, bạn An đi được 15km thì nghỉ một lúc. Hỏi bạn An còn phải đi tiếp tục mấy phần quãng đường nữa?
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
Bài 8: Quy đồng phân số rồi sắp xếp các phân số sau theo thứ tự tăng dần:
\(\dfrac{3}{4};\dfrac{2}{3} \;và \;\dfrac{19}{20}.\)
........................................................................................................................................
........................................................................................................................................
........................................................................................................................................
.........................................................................................................................................
Lời giải chi tiết
Bài 1:
Phương pháp giải:
Áp dụng kiến thức: Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.
Cách giải:
Trong các phân số đã cho, phân số có tử số bé hơn mẫu số là \(\dfrac{4}{5}\) (Vì 4 < 5).
Vậy đáp án đúng là C.
Bài 2:
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số: Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 ta thu được phân số mới bằng phân số đã cho.
Cách giải:
Áp dụng tính chất cơ bản của phân số ta có:
\(\dfrac{4}{7} = \dfrac{{4 \times 2}}{{7 \times 2}} = \dfrac{8}{{14}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)\(\dfrac{4}{7} = \dfrac{{4 \times 3}}{{7 \times 3}} = \dfrac{{12}}{{21}}\,\,;\)
\(\dfrac{4}{7} = \dfrac{{4 \times 4}}{{7 \times 4}} = \dfrac{{16}}{{28}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\)\(\dfrac{4}{7} = \dfrac{{4 \times 10}}{{7 \times 10}} = \dfrac{{40}}{{70}}\,.\)
Vậy ta có kết quả như sau :
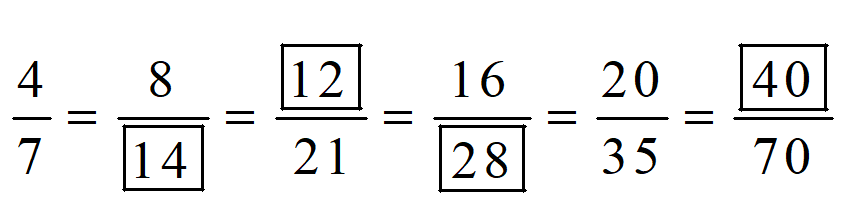
Bài 3:
Phương pháp giải:
• Trong hai phân số có cùng mẫu số:
- Phân số nào có tử số bé hơn thì bé hơn.
- Phân số nào có tử số lớn hơn thì lớn hơn.
- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
• Trong hai phân số cùng tử số:
- Phân số nào có mẫu số lớn hơn thì bé hơn.
- Phân số nào có mẫu số nhỏ hơn thì lớn hơn.
- Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Cách giải:
|
a) \(\dfrac{21}{75}<\dfrac{22}{75}\) |
b) \(\dfrac{21}{75}>\dfrac{22}{75}\) |
|
c) \(\dfrac{37}{26}<\dfrac{37}{27}\) |
|
Bài 4:
Phương pháp giải:
Phân số có mẫu số là 10, 100, 1000, ... gọi là phân số thập phân.
Cách giải:
Các phân số có mẫu số là 10, 100, 1000, ... gọi là phân số thập phân.
Vậy đáp án đúng là B.
Bài 5:
Phương pháp giải: Để giải bài toán ta thực hiện các bước sau:
- Tính số bút bi đen = tổng số bút – số bút xanh – số bút đỏ.
- Tìm phân số chỉ số bút xanh so với bút đen = \(\dfrac{số \;bút \;xanh}{số\; bút\; đen}\) .
- Tìm phân số chỉ số bút đỏ so với số bút đen =\(\dfrac{số \;bút\;đỏ}{số \;bút \;đen}\) .
Cách giải:
Số bút đen là:
\(35-12-10=13\) (bút)
Phân số chỉ số bút xanh so với bút đen là: \(\dfrac{12}{13}\).
Phân số chỉ số bút đỏ so với bút đen là: \(\dfrac{10}{13}\).
Đáp số:\(\dfrac{12}{13}\) ;\(\dfrac{10}{13}\) .
Bài 6:
Phương pháp giải:
Để làm được bài này ta phải nhớ các quy đổi và rút gọn phân số:
1cm =\(\dfrac{1}{100} \)m ; 1m =\(\dfrac{1}{1000}\) km ; 1 phút =\(\dfrac{1}{60}\) giờ.
Cách giải:
a) 45cm = \(\dfrac{{45}}{{100}}\)m = \(\dfrac{9}{{20}}\)m.
b) 225m = \(\dfrac{{225}}{{1000}}\)km = \(\dfrac{9}{{40}}\)km.
c) 15 phút = \(\dfrac{{15}}{{60}}\)giờ = \(\dfrac{1}{4}\) giờ.
Bài 7:
Phương pháp giải:
Để giải bài toán ta thực hiện các bước sau:
- Tính quãng đường còn lại mà bạn An phải đi = tổng quãng đường – quãng đường đã đi được.
- Bạn An còn phải đi tiếp tục mấy phần quãng đường chính là phân số giữa quãng đường còn lại so với tổng quãng đường =\(\dfrac{ quãng \;đường \;còn\; lại}{quãng \;đường \;phải \;đi}\) .
Cách giải:
Quãng đường còn lại bạn An phải đi là:
\(25-15=10\) (km)
Bạn An phải đi tiếp tục số phần đường là:
\(\dfrac{{10}}{{25}} = \dfrac{2}{5}\)(quãng đường)
Đáp số: \(\dfrac{2}{5}\) quãng đường.
Bài 8:
Phương pháp giải:
• Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
• Trong hai phân số có cùng mẫu số:
- Phân số nào có tử số bé hơn thì bé hơn.
- Phân số nào có tử số lớn hơn thì lớn hơn.
- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Cách giải:
Chọn mẫu số chung là 60.
Quy đồng mẫu số các phân số ta có:
\(\dfrac{3}{4} = \dfrac{{3 \times 15}}{{4 \times 14}} = \dfrac{{45}}{{60}}\); \(\dfrac{2}{3} = \dfrac{{2 \times 20}}{{3 \times 20}} = \dfrac{{40}}{{60}}\); \(\dfrac{{19}}{{20}} = \dfrac{{19 \times 3}}{{20 \times 3}} = \dfrac{{57}}{{60}}\).
Lại có \(\dfrac{{40}}{{60}} < \dfrac{{45}}{{60}} < \dfrac{{48}}{{60}}\) (vì (40 < 45 < 57\)).
Do đó: \(\dfrac{2}{3} < \dfrac{3}{4} < \dfrac{{19}}{{20}}\).
Vậy các phân số được sắp xếp theo thứ tự tăng dần là: \(\dfrac{2}{3}\); \(\dfrac{3}{4}\); \(\dfrac{{19}}{{20}}\).
Loigiaihay.com
Các bài khác cùng chuyên mục
- Bài tập cuối tuần Toán 5 tuần 7 - Đề 2 ( Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 33 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 33 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 35 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 35 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 2 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 34 - Đề 1 (Có đáp án và lời giải chi tiết)
- Bài tập cuối tuần Toán 5 tuần 33 - Đề 2 (Có đáp án và lời giải chi tiết)















Danh sách bình luận