Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - c..
Bài 38 trang 124 SGK Toán 7 tập 1
Trên hình 104 ta có AB//CD, AC//BD. Hãy chứng minh rằng AB=CD,AC=BD.
Đề bài
Trên hình \(104\) ta có \(AB//CD, AC//BD.\) Hãy chứng minh rằng: \(AB=CD;AC=BD.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc so le trong bằng nhau.
Lời giải chi tiết
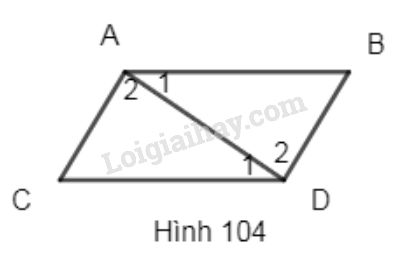
Vẽ đoạn thẳng \(AD.\)
Vì \(AB//CD\) suy ra \(\widehat{A_{1}}= \widehat{D_{1}}\) (hai góc so le trong)
Vì \(AC//BD\) suy ra \(\widehat{A_{2}}=\widehat{D_{2}}\) (hai góc so le trong)
Xét \(∆ADB\) và \(∆DAC\) có:
+) \(\widehat{A_{1}}= \widehat{D_{1}}\) (chứng minh trên)
+) \(AD\) cạnh chung
+) \(\widehat{A_{2}}=\widehat{D_{2}}\) (chứng minh trên)
\( \Rightarrow ∆ADB=∆DAC\) (g.c .g)
\(\Rightarrow AB=CD, BD=AC\) (các cạnh tương ứng)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 39 trang 124 SGK Toán 7 tập 1
- Bài 40 trang 124 SGK Toán 7 tập 1
- Bài 41 trang 124 SGK Toán 7 tập 1
- Bài 42 trang 124 SGK Toán 7 tập 1
- Bài 43 trang 125 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
