Đề kiểm tra 15 phút - Đề số 9 - Bài 2,3,4,5 - Chương 2 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 9 - Bài 2,3,4,5 - Chương 2 - Hình học 7
Đề bài
Cho tam giác ABC có ba góc nhọn, vẽ \(\widehat {EAF} = {120^o} \Rightarrow \widehat {AEF} = \widehat {AFE} = {30^o}. \) \(AH \bot BC\) (H thuộc BC). Từ H vẽ HI, HK lần lượt vuông góc với AB và AC, \(I \in AB,\,K \in AC.\) Trên tia đối của tia IH, KH lần lượt lấy các điểm E, F sao cho \(IE = IH\) và \(KF = KH.\)
a) Chứng minh \(AE = AF.\)
b) Giả sử cho \(\widehat {BAC} = {60^o}\). Hãy tính số đo các góc của \(\Delta AEF\).
Phương pháp giải - Xem chi tiết
a.Chứng minh các cặp tam giác bằng nhau: AIE và AIH, AKH và AKF
b.Sử dụng tính chất 2 tam giác bằng nhau và tính chất tam giác cân
Lời giải chi tiết
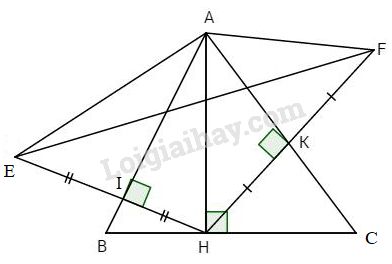
a) Xét \(\Delta AIE\) và \(\Delta AIH\) có:
+) AI là cạnh chung
+) \(\widehat {AIE} = \widehat {AIH} = {90^o}\) (giả thiết)
+) IE = IH (giả thiết)
Do đó \(\Delta AIE=\Delta AIH\) (c.g.c)
\( \Rightarrow AE = AH\) (1) (cạnh tương ứng)
Tương tự chứng minh
\(\Delta AKH = \Delta AKF \Rightarrow AH = AF\;\;(2)\)
Từ (1) và (2) \( \Rightarrow AE = AF.\)
b)Theo chứng minh trên ta có \(\widehat {EAI} = \widehat {HAI}\) và \(\widehat {HAK} = \widehat {FAK}.\)
mà \(\widehat {HAI} + \widehat {KAH} = \widehat {BAC} = {60^o}\)
\( \Rightarrow \widehat {EAI} + \widehat {HAI} + \widehat {HAK} + \widehat {FAK} \)\(\,= {120^o}\)
\(\Delta AEF\) cân có \(\widehat {EAF} = {120^o}\)
\(\Rightarrow \widehat {AEF} = \widehat {AFE} = {30^o}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 10 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 11 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 13 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 14 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 15 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
