Đề kiểm tra 15 phút - Đề số 17 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 17 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
Đề bài
Cho tam giác ABC, đường trung trực d1 của đoạn thẳng BC và đường trung trực d2 của đoạn thẳng AC cắt nhau tại O.
a) Chứng minh \(OA = OB = OC.\)
b) Gọi M là trung điểm của đoạn AB. Chứng minh OM là đường trung trực của đoạn AB.
Phương pháp giải - Xem chi tiết
-Điểm thuộc đường trung trực của đoạn thẳng thì cách đều 2 đầu mút
-Muốn chứng minh đường thẳng là đường trung trực của đoạn thẳng ta chứng minh nó đi qua trung điểm và vuông góc với đoạn thẳng đó
Lời giải chi tiết
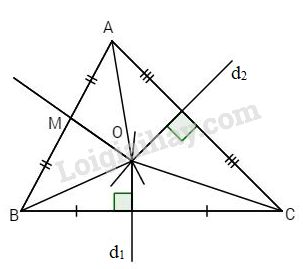
a) d1 là trung trực của đoạn thẳng BC\( \Rightarrow OB = OC\).
Tương tự d2 là trung trực của AC \( \Rightarrow OC = OA.\)
Do đó \(OA = OB = OC.\)
b) Xét \(\Delta OMA \) và \( \Delta OMB\) có
+) OM chung
+) OA = OB (chứng minh trên)
+) MA = MB (giả thiết).
Vậy \(\Delta OMA = \Delta OMB\) (c.c.c)
\( \Rightarrow \widehat {OAM} = \widehat {OMB}\) (góc tương ứng) mà \(\widehat {OAM} + \widehat {OMB} = {180^o}\) (cặp góc kề bù)
\( \Rightarrow \widehat {OAM} = \widehat {OMB} = {90^o}\).
Chứng tỏ \(OM \bot AB.\)
Mà M là trung điểm của AB. Do đó OM là đường trung trực của AB.
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 18 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 19 - Bài 2,3,4,5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 16 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 15 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
- Đề kiểm tra 15 phút - Đề số 14 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
