Bài 3 trang 43 SGK Hình học 10 nâng cao

LG a

\({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

Phương pháp giải:

Sử dụng đường tròn lượng giác và định lí Pitago trong tam giác vuông để chứng minh.

Lời giải chi tiết:

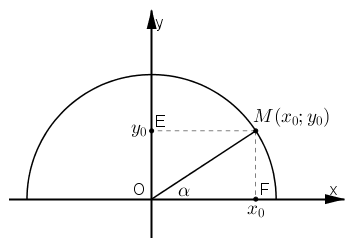
Vẽ nửa đường tròn lượng giác (O; 1).

Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x₀; y₀) thuộc nửa đường tròn sao cho \(\widehat {xOM} = \alpha \)

Khi đó ta có: sin α = y₀ ; cos α = x₀.

Mà M thuộc đường tròn lượng giác nên OM=1.

Ta có:

\(\begin{array}{l}
{\sin ^2}\alpha + {\cos ^2}\alpha = y_0^2 + x_0^2\\
= O{E^2} + O{F^2} = M{F^2} + O{F^2}\\
= O{M^2} = {1^2} = 1\\
\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1
\end{array}\)

Cách khác:

TH1: \(\alpha  = {0^0}\) thì \({\sin ^2}\alpha  + {\cos ^2}\alpha  = {\sin ^2}0^0 + {\cos ^2}0^0 \) \(=0^2+1^2= 1\)

TH2: \(\alpha  = {180^0}\) thì \({\sin ^2}\alpha  + {\cos ^2}\alpha  = {\sin ^2}180^0 + {\cos ^2}180 ^0\) \(=0^2+(-1)^2= 1\)

TH3: \(0^0 < \alpha  < {90^0}\).

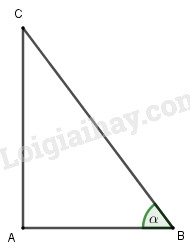
Xét tam giác \(ABC\) vuông tại \(A\), đặt \(\widehat B = \alpha \) có:

\(\sin \alpha  = \sin B = \dfrac{{AC}}{{BC}},\) \(\cos \alpha  = \cos B = \dfrac{{AB}}{{BC}}\)

\( \Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  \) \(= {\left( {\dfrac{{AC}}{{BC}}} \right)^2} + {\left( {\dfrac{{AB}}{{BC}}} \right)^2}\) \( = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \dfrac{{B{C^2}}}{{B{C^2}}} = 1\)

TH4: \({90^0} < \alpha  < {180^0}\).

\( \Rightarrow {0^0} < {180^0} - \alpha  < {90^0} \)

\(\Rightarrow {\sin ^2}\left( {{{180}^0} - \alpha } \right) + {\cos ^2}\left( {{{180}^0} - \alpha } \right)=1\) (áp dụng TH3)

\( \Rightarrow  {\sin ^2}\alpha  + {\left( { - \cos \alpha } \right)^2} =1\) (vì \(\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha ,\) \(\cos \left( {{{180}^0} - \alpha } \right) =  - \cos \alpha \))

\(\Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

Vậy ta có đpcm.

LG b

\(1 + {\tan ^2}\alpha  = {1 \over {{{\cos }^2}\alpha }}\,\,\,\,\,(\alpha  \ne {90^0})\)

Lời giải chi tiết:

\(1 + {\tan ^2}\alpha  = 1 + {{{{\sin }^2}\alpha } \over {{{\cos }^2}\alpha }} \)

\(= {{{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \over {{{\cos }^2}\alpha }} = {1 \over {{{\cos }^2}\alpha }}\,\)

LG c

\(1 + {\cot ^2}\alpha  = {1 \over {{{\sin }^2}\alpha }}\,\,\,\,\,({0^0} < \alpha  < {180^0})\)

Lời giải chi tiết:

\(1 + {\cot ^2}\alpha  = 1 + {{{{\cos }^2}\alpha } \over {{{\sin }^2}\alpha }} \)

\(= {{{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \over {{{\sin }^2}\alpha }} = {1 \over {{{\sin }^2}\alpha }}\,\)

Loigiaihay.com